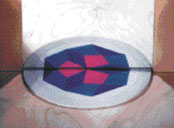
Podemos utilizar um espelho para verificar se uma recta é ou não um eixo de simetria para uma determinada figura, colocando-o ao longo da recta em questão, perpendicularmente ao plano da figura: se a recta é um eixo de simetria, como na figura 1, então a metade da figura, juntamente com a imagem reflectida, reconstrói uma figura idêntica à inicial (ver figura 2), caso contrário, tal não se verifica.

 

fig 1	fig 2	fig 3	fig 4

E, conforme podemos observar nas imagens 3 e 4, isto pode efectivamente não acontecer mesmo que a recta em questão divida a figura em duas partes iguais.

Mas o que acontece se utilizarmos dois espelhos? Imaginemos por exemplo, que introduzimos um p entre dois espelhos paralelos (a região entre os dois espelhos está representada na figura abaixo a amarelo): podemos então observar uma série de imagens que se repetem ao longo de uma linha, alternando imagens do p com imagens do q.

Nota: Para manipular a letra P, clique sobre a imagem

Se efectuarmos primeiro uma reflexão em relação a uma recta e depois uma outra reflexão em relação a uma outra recta, paralela à primeira, o efeito obtido corresponde ao de uma translação, numa direcção perpendicular às duas rectas e deslocamento igual ao dobro da distância entre essas duas rectas.

Qualquer reflexão troca a direita com a esquerda: de facto, a imagem no espelho de um p, que tem a perna à esquerda, é um q, com a perna à direita. Uma translação, pelo contrário, equivale a duas reflexões, logo... a perna do p mantém-se no seu devido lugar.

E se os eixos não forem rectas paralelas mas sim concorrentes?