Se não conhece o jogo, veja a sua descrição nas páginas sobre o módulo existente na Exposição Matemática Viva, para o caso de 3 cores ou recorra a um applet feito com o JavaSketchpad.
    Em cada figura do quadro abaixo, há um apontador para um applet, que simula o lançamento de um dado com três cores (primeiros 5 triângulos), quatro cores (2 quadrados) e cinco cores (2 pentágonos). De cada vez que «clica» num dos applets, são simulados uns milhares de lançamentos de dado e marcados os respectivos pontos. Sucessivos «cliques» não conduzem exactamente à mesma figura, como poderá detectar se observar cuidadosamente, mas o tipo das figuras sucessivas é muito semelhante, em cada caso.
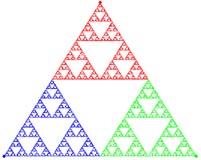
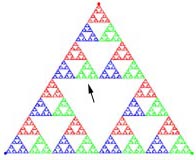
    As cores, nas figuras, representam o seguinte: no primeiro triângulo, cada ponto tem a cor saída no (último) lançamento do dado, que lhe deu origem, no segundo triângulo tem a cor saída no penúltimo lançamento do dado, etc. Assim, por exemplo, observando os três triângulos da primeira linha da tabela, concluímos que, no terceiro desses triângulos, i.e., o que está mais à direita, para todos os pontos do pequeno triângulo verde assinalado com a seta, o último lançamento do dado saiu vermelho, o penúltimo azul e o antepenúltimo verde. 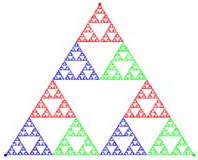Portanto, todos os pontos desse pequeno triângulo verde assinalado com a seta têm a mesma «história» recente. Para conhecermos, a partir da posição final desses pontos, qual a história mais antiga dos lançamentos, poderemos observar como os pontos desse triângulo verde estão pintados nos dois triângulos que se seguem (na segunda linha do quadro).
    Dado que as diferentes histórias são igualmente prováveis, e cada história está associada à posição do ponto pela forma que as figuras sugerem, podemos perceber por que razão os pontos estão igualmente distribuídos no triângulo de Sierpinski, isto é, por que razão a probabilidade de um ponto ir parar a uma zona só depende do «tamanho» dessa zona.
 
 

    Nos casos de 4 pontos e de 5 pontos, com regras semelhantes, pode-se observar algumas diferenças relativamente ao caso mais simples dos três pontos: nos quadrados não há «buracos» e, no caso dos cinco pontos, volta a haver buracos, mas há zonas mais escuras, de sobreposição. Procure descobrir a razão para estas diferenças e, depois, conjecture o que sucederá se tivermos 6 ou 7 pontos. E que lhe parece que sucede em todos estes casos, quanto à probabilidade de os pontos irem parar às diferentes zonas da figura?