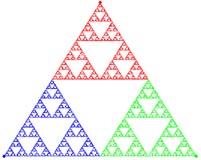
Atractor de Sierpinski
(notas)
OBS. 1 - «...no primeiro
triângulo, cada ponto tem a cor saída no (último) lançamento
do dado...»

Na verdade, a afirmação deve ser vista
para «todos» os pontos, excepto três, em que a cor a
priori poderia ser uma de duas: são os vértices comuns
aos triângulos azul e verde, azul e vermelho e verde e vermelho.
Nestes, não é claro qual a cor na figura. E essa ambiguidade
corresponde também a uma aparente impossibilidade
de, somente a partir da posição do ponto, determinar a sua
«história», mesmo recente. Por exemplo, o primeiro destes
três pontos - vértice comum aos triângulos azul e verde
- tanto pode ser obtido com um lançamento inicial azul e um segundo
verde (caso em que o último lançamento foi verde) como com
um inicial verde e um segundo azul (caso em que o último lançamento
foi azul).
OBS. 2 - «...para todos os pontos do pequeno triângulo verde assinalado com a seta, o último lançamento do dado saiu vermelho, o penúltimo azul e o antepenúltimo verde. Portanto, todos os pontos desse pequeno triângulo verde assinalado com a seta têm a mesma história recente.»
De facto, também aqui, «todos» deve excluir a priori, pelas mesmas razões, os vértices do pequeno triângulo assinalado com a seta. Relativamente a estes três vértices, a situação é a seguinte:
OBS. 3 - «Para conhecermos, a partir da posição final desses pontos (do triângulo assinalado com a seta),
qual a história mais antiga dos lançamentos, poderemos observar como os pontos desse triângulo verde estão pintados nos dois triângulos que se seguem (na segunda linha do quadro)»
Na verdade, mais uma vez, observar estes dois grandes triângulos
do quadro permite alargar o conhecimento da história dos lançamentos
a mais duas gerações, para todos os pontos (menos a priori
os
três vértices) do pequeno triângulo verde assinalado
com a seta, com algumas (12=3+9) aparentes excepções
novas - os vértices dos novos triângulos mais pequenos.
OBS. 4 - As reservas
feitas nas observações anteriores sobre os aparentes
pontos excepcionais (vértices), relativamente aos quais não
era a priori possível conhecer a história dos
lançamentos que lhe deram origem, não tiveram em conta um
conhecimento suplementar, que é suficiente para desfazer qualquer
ambiguidade. É o raciocínio subjacente (algo subtil), que
expomos a seguir.
No jogo, parte-se de um dos vértices do triângulo
inicial - azul, verde ou vermelho -, eventualmente tirado à sorte:
suponhamos que é o da esquerda (azul); se for outro, o raciocínio
é análogo. Se o primeiro foi azul, nenhum ponto do lado oposto
(tendo os pontos verde e vermelho por extremos) pode vir a ser obtido (basta
atender a que o ponto médio de um segmento que une um ponto do triângulo
que não esteja naquele lado, a um dos extremos desse lado, não
está nesse lado). Então, não é difícil
concluir que também nenhum ponto de qualquer outro lado paralelo
àquele, dos pequenos triângulos (das figuras seguintes do
quadro), pode também ser obtido. Portanto, em cada pequeno triângulo,
dos que se vão formando por marcação sucessiva
dos pontos, há, no máximo, um vértice marcado e esse
vértice ocupa, relativamente ao triângulo adjacente de que
tem a cor, a mesma posição que o ponto inicial (azul, no
caso que estamos a considerar) ocupava relativamente ao triângulo
inicial. (No caso que estamos a considerar - de o lançamento inicial
ter sido azul - um vértice marcado tem a cor daquele dos dois triângulos
adjacentes que está à direita desse vértice e há
sempre um tal pequeno triângulo, porque nenhum ponto marcado está
num lado paralelo ao lado direito do triângulo grande.)
Portanto, e resumindo, não há ambiguidade
nenhuma desde que se conheça o primeiro ponto marcado. Mas, pelas
considerações feitas, este ponto é exactamente o único
dos vértices do triângulo grande que foi marcado.