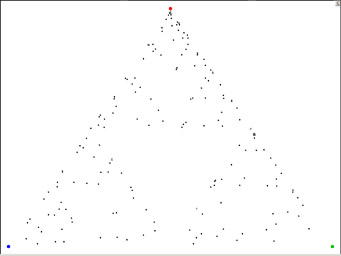
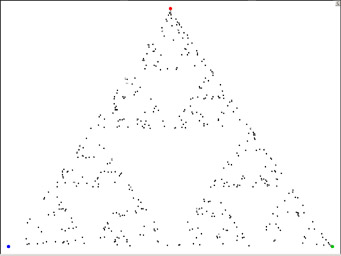
Eis o aspecto, em Fevereiro de 2001, da imagem do Atractor de Sierpinski:

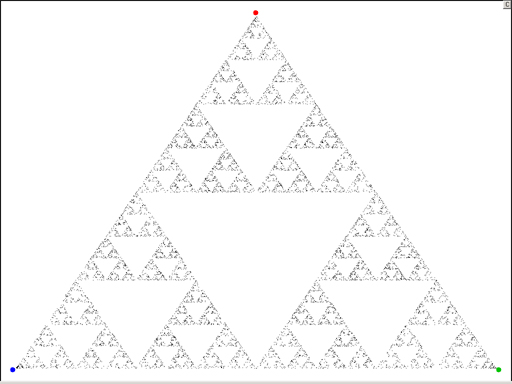
Foi obtida com os pontos construídos a partir dos lançamentos de um dado atirado pelos sucessivos visitantes desde 24 de Novembro de 2000.
Cada visitante, ao carregar num botão, desencadeia o seguinte  processo:

1. o dado é lançado
2. a cor (azul, verde, vermelho) do dado é reconhecida automaticamente
3. é desenhado o segmento que une a posição do último ponto marcado ao vértice com a cor que saiu
4. é acresentado ao desenho o ponto médio desse segmento
5. é apagado o segmento e fica marcado o último ponto acrescentado.

Eis os aspectos da figura em algumas fases iniciais:
 
 

Se, em vez de se tomar como primeiro ponto um dos três vértices do triângulo, se tomasse um qualquer ponto do plano, o aspecto da figura obtida (desprezando um número suficiente de pontos iniciais) seria muito semelhante ao que está representado na figura de cima. O triângulo de Sierpinski, que contem a figura acima, é um atractor para o processo descrito, em particular,  as distâncias a esse conjunto dos sucessivos pontos obtidos a partir de um qualquer ponto do plano, tendem para 0.

Algumas questões interessantes e relacionadas:

1. Será que a frequência com que os pontos caem em cada «pequeno triângulo» é a mesma ou será que há zonas de maior concentração? (É possível concluir que a repartição é uniforme.)
2. E se tivessemos aplicado um processo análogo a um quadrado? (Ou a um pentágono regular ou a um hexágono regular, ...?)
3. As conclusões seriam essencialmente diferentes se os polígonos de partida fosem não regulares? (Por exemplo, um triângulo escaleno ou um quadrilátero qualquer.)

N.B. - Pode encontrar aqui alguma informação suplementar sobre estes pontos.