Toro - grupo fundamental
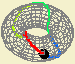
No toro (leia-se, na superfície do toro), o tratamento das homotopias não é tão simples como no plano. Atentemos, por exemplo, no caminho fechado que dá uma volta à superfície sobre um paralelo. Impossibilitados de mover os pontos inicial e final, não vai ser possível contrair esse caminho num ponto, portanto esses dois caminhos (o arco fechado e o ponto) não são homotópicos. Analogamente, considerando um caminho fechado que dá uma volta ao longo de um meridiano, também não é possível a contracção. Estas ideias podem ser exploradas intuitivamente na app.
Tendo em conta estes dois exemplos e após uma exploração mais generalizada da app, o que pode concluir sobre a possibilidade de homotopia dos caminhos sobre o toro?
Uma conclusão importante é que depende do "número líquido de voltas" em cada direcção. De facto, mostra-se que essa é a única condição. Dados dois caminhos e calculado o "número líquido de voltas" em cada direcção (considerando os caminhos fechados obtidos, se necessário, pelo completamento com um arco que une o ponto final ao ponto inicial), existe homotopia se e só se esses números de voltas forem respectivamente iguais.
Assim, no toro, considerando os caminhos fechados, uma classe de homotopia pode ser caracterizada por um par de números inteiros (n.º de voltas longitudinais, n.º de voltas latitudinais). Desta forma, dizemos que há uma correspondência entre o conjunto das suas classes de homotopia e o conjunto dos pares de inteiros - o grupo fundamental do toro é isomorfo a \(\mathbb{Z}\times\mathbb{Z}\).
Esta correspondência também pode ser explicada no levantamento no plano. Escolhido um ponto do toro e um dos seus levantamentos no plano, cada caminho fechado no toro admite um único levantamento cuja origem seja o ponto escolhido do plano. Então, a classe de equivalência do caminho fechado no toro fica determinada pelo ponto de chegada do levantamento no plano; ponto que pode tomar uma infinidade numerável de valores, cada um determinado por um par de números inteiros (a sua posição à direita ou à esquerda, acima ou abaixo do original).