Esfera - grupo fundamental
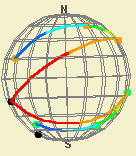
Na esfera (leia-se, superfície esférica!), à semelhança do plano, também quaisquer dois caminhos com os mesmos pontos inicial e final são homotópicos. Agora as famílias de caminhos consideradas podem ser arcos que unem os pontos do primeiro caminho aos pontos do segundo. Uma forma de obter esta conclusão resulta de ter em conta a projecção estereográfica entre a esfera e o plano: considerar um ponto da esfera (pólo de projecção) e o plano tangente ao ponto diametralmente oposto e associar a cada ponto da esfera o ponto do plano que resulta da intersecção da semi-recta que parte do pólo e passa no ponto. Esta projecção estabelece uma correspondência biunívoca entre o plano e a esfera (menos o pólo de projecção). Assim, escolhendo como pólo um ponto que não pertença a qualquer dos caminhos (considerando, se necessário, uma homotopia que o permita), e uma vez que a projecção mantem a continuidade e a incidência, podemos estabelecer uma correspondência entre caminhos na esfera e caminhos no plano. Dados dois caminhos na esfera, podemos projectá-los no plano, considerar a homotopia que aí existe entre eles (associada, por exemplo, a uma família de segmentos de recta) e projectá-la na esfera (associando-se a uma família de arcos de circunferência).
Assim, na esfera, como no plano, todos os caminhos são homotópicos, havendo, portanto, apenas uma classe de homotopia.
E, também como no plano, analisando o grupo fundamental, podemos concluir que todos os caminhos (fechados) são homotópicos a um caminho constante - que, por simplicidade, pode ser tido como representante da classe (única).