Torus - fundamental group
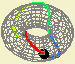
In the torus, the study of homotopies is not as simple as in the plane. For example, consider the closed path which follows around the surface along a longitude. As the path is closed, in this case it is not possible to contract the path into a point; the two paths (the point and the closed path) are not homotopic. Similarly, a closed path which follows the torus along the meridian is also not contractible into a point. these ideas can be explored intuitively in the app.
Taking into acount these two examples and the experience from the interaction with the app, what can we conjecture about the homotopies of paths in the torus?
One important observation is that it depends on the "number of times it goes around" the torus in each direction. In fact, we can show this is the only condition. Given two paths and computing their "number of times around" the torus in each direction (consider, if necessary, the closed paths obtained by completing the paths by an arc joining the start and end points of each), there is a homotopy between the two paths if and only if the number of times around the torus is the same.
Hence, considering the closed paths in the torus, one homotopy class can be characterized by a pair of integers (number of times around the longitude and meridian of the torus). In this way, we say that there is a correspondence between the set of homotopy classes and the pair of integer set - the fundamental group of the torus is isomorphic to \(\mathbb{Z}\times\mathbb{Z}\).
This correspondence can be explained through the lift of the torus to the plane. Chosen a point in the torus and one point among its lifts in the plane, each closed path in the torus admits a single lift with start point the chosen point. Therefore, the equivalence class of the closed path in the torus is determined by the end point of its lift in the plane; a point which can take an infinitude of values, each determined by a pair of integral numbers (with respect to its position to the right or left, above or below, the start point).