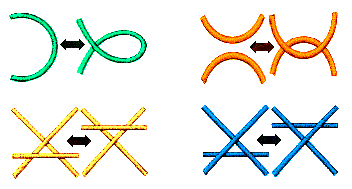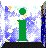Decomposição em Elementos Simples
Decomposição em elementos simples é um processo básico
em Matemática, ou de facto sempre que se trata de assuntos complicados.
Em teoria dos nós este processo aparece de uma variedade de maneiras.
- Já mencionámos a decomposição prima de nós. Aqui os nós primos
são os elementos simples e o facto que qualquer nó se pode exprimir de
maneira única (a menos da ordem) como soma de nós primos é claramente
um facto importante sobre nós.
- O processo de transformar um diagrama de nó noutro pode ser
bastante complicado. É portanto interessante que um processo tão
complexo possa ser decomposto numa sequência de algum dos
quatro tipos de mudanças de cruzamentos simples, os movimentos
de Reidemeister
juntamente com deformações
sem alterar os cruzamentos. Ilustrámos isto ao modificar o
nó de cadeira
e também ao mostrar porque é que a
colorabilidade de um nó é um invariante.
Há uma infinidade de sequências de movimentos que se podem
efectuar sobre um diagrama. É por isso que pode ser tão difícil
decidir se dois diagramas representam ou não o mesmo nó. Se
representarem o mesmo nó, pode ser difícil decidir qual é
o menor número de movimentos que pode ser usado para transformar
um diagrama noutro.
©Mathematics and Knots, U.C.N.W.,Bangor,
1996.
Este material pode ser empregue sem restrições para fins educacionais,
artísticos e científicos, citando a fonte, mas não pode ser empregue para fins comerciais
ou lucrativos ou em textos sem a autorização dos responsáveis.