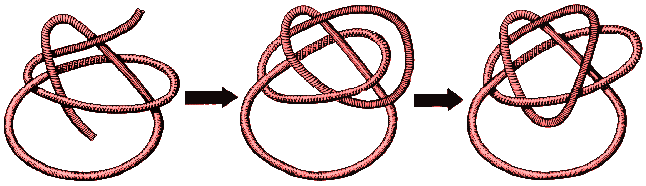

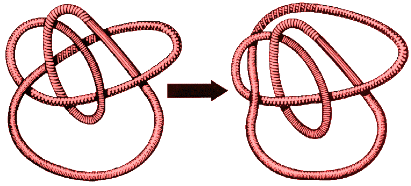
 Se juntarmos as pontas, podemos mexer no fio através de várias posições até
ele se cruzar a si próprio apenas seis vezes. A versão de seis cruzamentos
do nó de cadeira é a representação mais simples possível deste nó.
Dizemos que o nó de cadeira tem número de cruzamento 6.
Se juntarmos as pontas, podemos mexer no fio através de várias posições até
ele se cruzar a si próprio apenas seis vezes. A versão de seis cruzamentos
do nó de cadeira é a representação mais simples possível deste nó.
Dizemos que o nó de cadeira tem número de cruzamento 6. |
Pode ser muito difícil distinguir dois
diagramas de nós complicados. Com apenas quatro movimentos pode-se
tornar um nó irreconhecível. Em 1899 uma tabela de nós foi feita
por C. M. Little. Os dois nós representados em baixo figuravam como
diferentes. Só em 1974 é que K. M. Perko descobriu que os dois nós
eram o mesmo. 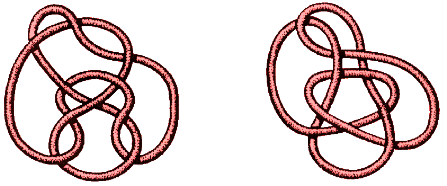 Uma tarefa
que os matemáticos enfrentam é encontrar maneiras
seguras de descobrir se dois nós são diferentes ou apenas versões
deformadas um do outro. A teoria dos nós apresenta-nos muitos
desafios destes. Uma tarefa
que os matemáticos enfrentam é encontrar maneiras
seguras de descobrir se dois nós são diferentes ou apenas versões
deformadas um do outro. A teoria dos nós apresenta-nos muitos
desafios destes. |
 Classificação
Classificação