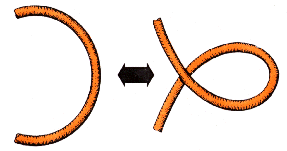
de ambos os lados |
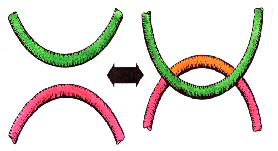
e à esquerda não temos nenhum cruzamento |
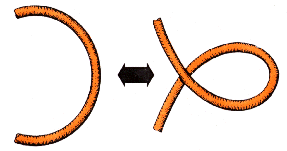
de ambos os lados |

e à esquerda não temos nenhum cruzamento |
Mostramos em baixo dois dos numerosos casos que envolvem um terceiro tipo de movimento. Note que somos sempre autorizados a mudar algumas cores num movimento, mas temos de respeitar a regra básica: em cada cruzamento tem de haver ou uma cor ou três cores. Isto pode ser feito para cada movimento. Portanto vemos que uma figura que não é 3-colorível não pode ser um trevo disfarçado.

|

|
|---|
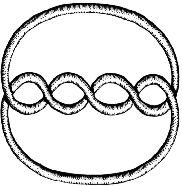
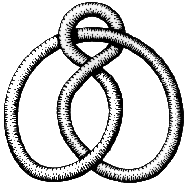
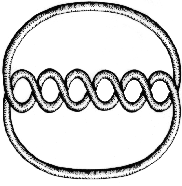
E quanto a outras maneiras de colorir? É interessante experimentar com mais de 3 cores, do mesmo modo, mas descobriu-se que isto não dá directamente um invariante do nó. Em vez disso tem de se usar um tipo de etiquetagem mais subtil que fornece novos invariantes. Tente experimentar com diversas maneiras de colorir os nós seguintes e outros diagramas deles.
|
|
|
|---|
 Invariantes
Invariantes