PARA SABER MAIS...
Existem várias definições de curva no sentido matemático. Por exemplo, podemos pensar numa curva enquanto conjunto de pontos que verificam uma determinada condição, como por exemplo uma circunferência. Contudo, ser-nos-á mais útil adoptar um outro tipo de definição: a de curva enquanto parametrização de um conjunto (esta parametrização pode, por exemplo, ter origem na descrição do movimento de uma partícula).
Neste trabalho, definimos curva como uma função \(\gamma:\,I\rightarrow\mathbb{R}^{3}\), onde \(I\subseteq\mathbb{R}\) é um intervalo, que a cada valor do parâmetro \(t\in I\) faz corresponder um ponto \(\gamma\left(t\right)\in\mathbb{R}^{3}\). Supomos ainda que as curvas são suaves, isto é, admitem derivadas de todas as ordens.
O contradomínio da curva é denominado por traço da curva. Note-se que diferentes curvas, isto é, com parametrizações diferentes, podem ter o mesmo traço.
As parametrizações das curvas loxodrómicas usadas neste trabalho dependerão da colatitude ou da longitude, ou seja, a posição de um ponto da curva dependerá univocamente da sua colatitude ou da sua longitude.
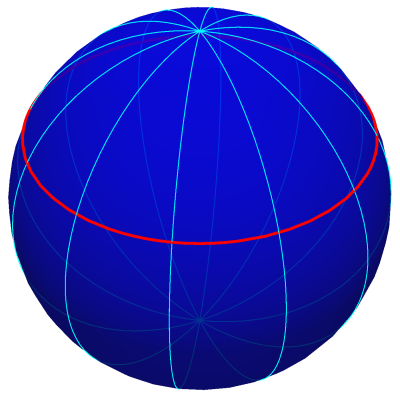
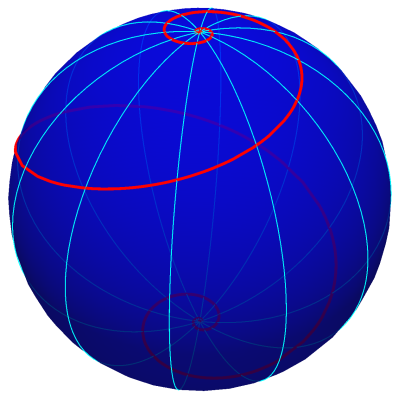
A curva loxodrómica é uma curva na esfera cuja característica essencial é fazer um ângulo constante com todos os meridianos que intersecta. Dois casos distintos podem surgir: a curva loxodrómica ser perpendicular aos meridianos e, neste caso, a sua parametrização será dada em função da longitude (θ); nos casos restantes, a parametrização será dada em função da colatitude (φ).
Considere-se a esfera com centro na origem O do refeferencial Oxyz e raio r > 0. Designaremos esta esfera por \(\mathbb{S}^{2}\).
Seja \(\ell_{\alpha}\) uma curva loxodrómica cujo ângulo de intersecção com os meridianos é \(\alpha\). Considere-se um ponto P fixo mas arbitrário do traço de \(\ell_{\alpha}\), com coordenadas esféricas \((r,\theta_{P},\varphi_{P})\).
Seja m o meridiano que intersecta a curva \(\ell_{\alpha}\) no ponto P . Uma parametrização do meridiano m que passa em P é a seguinte:
O meridiano m e a curva \(\ell_{\alpha}\) intersectam-se em P fazendo um ângulo com amplitude \(\alpha\). Consideremos dois casos distintos: no primeiro, suponhamos \(\alpha=\frac{\pi}{2}+n\pi\), para algum \(n\in\mathbb{Z}\), ou seja, a curva \(\ell_{\alpha}\) é perpendicular aos meridianos; no segundo caso, consideremos \(\alpha\neq\frac{\pi}{2}+n\pi\), para todo \(n\in\mathbb{Z}\).
| 1. \(\alpha=\frac{\pi}{2}+n\pi\), para algum \(n\in\mathbb{Z}\) Como
a curva loxodrómica é perpendicular aos meridianos, a sua parametrização
será dada em função da longitude, ou seja,
$$\ell_{\alpha}\left(\theta\right)=\left(r\cos\theta\sen\left(\varphi(\theta)\right)\,,\,r\sen\theta\sen\left(\varphi(\theta)\right)\,,\, r\cos\left(\varphi(\theta)\right)\right),$$ onde a colatitude
\(\varphi\) é uma função do parâmetro \(\theta\), \(\varphi:\,\left[0\,,2\pi\right]\rightarrow\
]0\,,\pi[\).
O ângulo entre duas curvas na esfera pode ser determinado calculando o ângulo entre os vectores tangentes às respectivas curvas no ponto de intersecção e este, por sua vez, pode ser obtido através do produto escalar dos dois vectores. Como
\(\ell_{\alpha}\) e m são perpendiculares em P,
então \(\ell_{\alpha}^{\prime}\left(\theta_{P}\right)\,|\, m'\left(\varphi_{P}\right)=0\).
Note-se
que \(\varphi(\theta_{P})=\varphi_{P}\). |
||
|
Temos
que: $$\begin{array}{rccl}
\ell_{\alpha}^{\prime}(\theta_{P}) & = & & r\,\varphi'\left(\theta_{P}\right)\left(\cos\left(\varphi_{P}\right)\cos\left(\theta_{P}\right)\,,\cos\left(\varphi_{P}\right)\sen\left(\theta_{P}\right)\,,\,-\sen\left(\varphi_{P}\right)\right)\\ & & + & r\left(-\sen\left(\theta_{P}\right)\sen\left(\varphi_{P}\right)\,,\,\cos\left(\theta_{P}\right)\sen\left(\varphi_{P}\right),0\right) \end{array}$$ e $$m'(\varphi_{P})=r\left(\cos\left(\varphi_{P}\right)\cos\left(\theta_{P}\right)\,,\,\cos\left(\varphi_{P}\right)\sen\left(\theta_{P}\right)\,,\,-\sen\left(\varphi_{P}\right)\right)\,.$$ Fazendo alguns
cálculos, obtém-se \(\varphi'(\theta_{P})=0\).
Sendo P um ponto arbitrário do traço de \(\ell_{\alpha}\), vem que \(\varphi(\theta)\) é constante e, fazendo a substituição \(\varphi(\theta_{P})=\varphi_{P}\), obtemos \(\varphi\left(\theta\right)=\varphi_{P}\). Portanto,
se \(\alpha=\frac{\pi}{2}+n\pi\), uma parametrização de \(\ell_{\alpha}\)
é dada por: $$\begin{array}{ccll} Neste
caso, o traço da curva \(\ell_{\alpha}\) corresponde a um paralelo
com colatitude igual a \(\varphi_{P}\). |
|
|
Note-se que, ao contrário
do que é sugerido pela notação, a curva \(\ell_{\alpha}\)
apresentada depende não só de \(\alpha\) como também
de \(\varphi_{P}\). Optou-se por este abuso de notação
para simplificar a escrita.
|
||
2. \(\alpha\neq\frac{\pi}{2}+n\pi\), \(n\in\mathbb{Z}\) Neste
caso, a parametrização de \(\ell_{\alpha}\) será dada em função
da colatitude* \(\varphi\in\ ]0\,,\pi[\): $$\begin{array}{ccll} com a longitude \(\theta_\alpha\) a depender do parâmetro \(\varphi\), \(\theta_\alpha:\ ]0\,,\pi[\rightarrow\mathbb{R}\). Como
já foi referido no ponto anterior, o ângulo entre duas curvas
na esfera corresponde ao ângulo entre os vectores tangentes
às respectivas curvas no ponto de intersecção. Assim, $$\cos\alpha=\frac{\ell_{\alpha}^{\prime}\left(\varphi_{P}\right)\,|\,m'\left(\varphi_{P}\right)}{\Vert\ell_{\alpha}^{\prime}\left(\varphi_{P}\right)\Vert\times\Vert |
||
|
Temos
que: $$\begin{array}{rccl} |
|
|
Se \(\alpha\) for múltiplo inteiro de \(\pi\), então \(\theta'_\alpha(\varphi)=0\) para todo \( \varphi \). Se \(\alpha\) não for múltiplo inteiro de \(\pi\), \(|\theta'_\alpha(\varphi_{P})|\geq|\tg\alpha|>0\), logo \(\theta'_\alpha\) terá sinal constante. Por considerações de carácter geométrico, escolhemos \(\theta'_\alpha(\varphi)=-\frac{\tg\alpha}{\sen\varphi}\) para \( \varphi \in ]0\,,\pi[\). Integrando em ordem a \(\varphi\), vem que \(\theta_\alpha(\varphi)=\tg\alpha\ln\left(\cotg\frac{\varphi}{2}\right)+k\), para alguma constante \(k\in\mathbb{R}\). Como \(\theta_\alpha(\varphi_{P})=\theta_{P}\), tem-se que \(k=\theta_{P}-\tg\alpha\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\). Portanto,
se \(\alpha\neq\frac{\pi}{2}+n\pi\), com \(n\in\mathbb{Z}\),
uma parametrização de \(\ell_{\alpha}\) é dada por: $$\begin{array}{ccll}
com \(\theta_\alpha(\varphi)=\theta_{P}+\tg\alpha\left[\ln\left(\cotg\frac{\varphi}{2}\right)- Note-se que, quando \(\alpha=0\), o traço da curva coincide com um meridiano (sem os pólos) pois, nesse caso \( \theta_\alpha\) é constante, \(\theta_\alpha(\varphi)=\theta_{P}\). Nos restantes casos (\(\alpha\neq\frac{\pi}{2}+n\pi\), com \(n\in\mathbb{Z}\)), o traço da curva loxodrómica assume a forma de uma espiral em torno dos pólos pois, quando \(\varphi\rightarrow0^{+}\) ou quando \(\varphi\rightarrow\pi^{-}\), \(\theta_\alpha(\varphi)\rightarrow\infty\), de onde se conclui que a curva dá infinitas voltas em torno do eixo dos zz. Apesar de já termos visto que, se a curva for regular (isto é, se a sua velocidade for sempre não nula), os pólos não podem pertencer ao traço da curva (supondo que a propriedade da curva fazer ângulo constante com os meridianos se mantém), é possível estender a curva loxodrómica de modo a conter os pólos. De facto, se \(\alpha\neq\frac{\pi}{2}n\), \(n\in\mathbb{Z}\), apesar de \(\lim_{\varphi\rightarrow0^{+}} \theta_\alpha\left(\varphi\right)=\pm\infty\) e de \(\underset{\varphi\rightarrow\pi^{-}}{\lim}\theta_\alpha\left(\varphi\right)=\pm\infty\), \(\underset{\varphi\rightarrow0^{+}}{\lim}\ell_{\alpha}\left(\varphi\right)=\left(0,0,r\right)\) e \(\underset{\varphi\rightarrow\pi^{-}}{\lim}\ell_{\alpha}\left(\varphi\right)=\left(0,0,-r\right)\). Logo, é possível estender \(\ell_{\alpha}\) a \(\left[0\,,\pi\right]\) de forma contínua. No entanto, essa nova curva não tem a propriedade de fazer ângulo constante com os meridianos que intersecta, precisamente nos pontos com \(\varphi=0\) e \(\varphi=\pi\) correspondentes aos pólos. |
||
| *Note-se
que, se \(\alpha\neq\frac{\pi}{2}+n\pi\), para todo \(n\in\mathbb{Z}\),
então não haverá dois pontos da curva com a mesma colatitude.
|