A curva loxodrómica e duas projecções da esfera

PARA SABER MAIS...

COMPRIMENTO DA CURVA LOXODRÓMICA

A função comprimento de arco de uma curva \(\gamma:\, I\rightarrow\mathbb{R}^{n}\), onde I é um intervalo real e \(t_{0}\in I\) é fixo, é uma função \(c:\, I\rightarrow\mathbb{R}\) definida por $$c(t)=\int_{t_{0}}^{t}\Vert\gamma'(x)\Vert\, dx\,.$$ O comprimento da curva \(\gamma:\,[a\,,b]\rightarrow\mathbb{R}^{n}\) é dado por $$\int_{a}^{b}\Vert\gamma'(x)\Vert\, dx\,.$$ Seja \(\ell_{\alpha}\) uma curva loxodrómica que faz um ângulo de amplitude \(\alpha\) com os meridianos que intersecta e cujo traço contém o ponto P de coordenadas esféricas \(\left(r,\theta_{P},\varphi_{P}\right)\), com \(\theta_{P}\in[0\,,2\pi]\), \(\varphi_{P}\in\ ]0\,,\pi[\) e \(r\) igual ao raio da esfera. De acordo com a parametrização de \(\ell_{\alpha}\), temos que considerar dois casos distintos: \(\alpha=\frac{\pi}{2}+n\pi\), para algum \(n\in\mathbb{Z}\), e \(\alpha\neq\frac{\pi}{2}+n\pi\), com \(n\in\mathbb{Z}\).

1. \(\alpha=\frac{\pi}{2}+n\pi\), para algum \(n\in\mathbb{Z}\)

Uma parametrização de \(\ell_{\alpha}\) é dada por: $$\begin{array}{ccll}
\ell_{\alpha}: & [0\,,2\pi] & \longrightarrow & \mathbb{S}^{2}\\ & \theta & \mapsto & \left(r\cos\theta\sen\left(\varphi_{P}\right)\,,\,r\sen\theta\sen\left(\varphi_{P}\right)\,,\,r\cos\left(\varphi_{P}\right)\right)
\end{array}\,.$$ Neste caso, o comprimento da curva \(\ell_{\alpha}\) é dado por $$\int_{0}^{2\pi}\Vert\ell_{\alpha}^{\prime}(\theta)\Vert\, d\theta\,.$$ Temos que $$\ell_{\alpha}^{\prime}(\theta)=r\left(- \sen\theta\sen\left(\varphi_{P}\right)\,,\,\cos\theta\sen\left(\varphi_{P}\right)\,,\,0\right)\,.$$ Calculando \(\Vert\ell_{\alpha}^{\prime}(\theta)\Vert^{2}\) obtém-se $$\Vert\ell_{\alpha}^{\prime}(\theta)\Vert^{2}=r^{2}\sen^{2}\left(\varphi_{P}\right)\,.$$ Como \(\sen\left(\varphi_{P}\right) > 0\), pois \(\varphi_{P}\in\,]0,\pi[\), vem que \(\Vert\ell_{\alpha}^{\prime}(\theta)\Vert=r\sen\left(\varphi_{P}\right)\).

Então, o comprimento da curva \(\ell_{\alpha}\) é dado por $$\int_{0}^{2\pi}r\sen\left(\varphi_{P}\right)d\theta=2\pi r\sen\left(\varphi_{P}\right)\,.$$

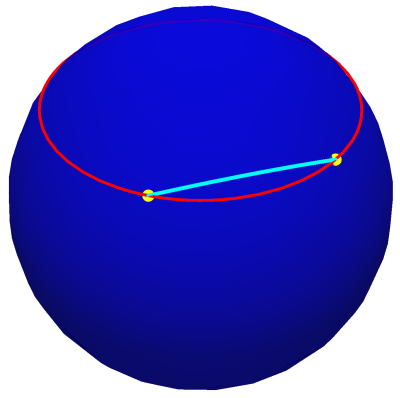
A vermelho está representada uma curva loxodrómica cujo traço corresponde a um paralelo. A azul está assinalado o caminho mais curto entre os dois pontos (menor arco de círculo máximo que os contém).

Note-se que, como neste caso o traço da curva \(\ell_{\alpha}\) corresponde a um paralelo com colatitude igual a \(\varphi_{P}\), poderíamos ter calculado o seu comprimento determinando o perímetro da circunferência de raio \(r\sen\left(\varphi_{P}\right)\).

Em particular, o comprimento do arco da curva \(\ell_{\alpha}\) entre dois pontos quaisquer da curva \(Q\,\left(r,\theta_{Q},\varphi_{P}\right)\) e \(R\,\left(r,\theta_{R},\varphi_{P}\right)\) é igual ao comprimento do correspondente arco de circunferência de raio \(r\sen\left(\varphi_{P}\right)\), com valor \(\left|\theta_{Q}-\theta_{R}\right|r\sen\left(\varphi_{P}\right)\).

2. \(\alpha\neq\frac{\pi}{2}+n\pi\), \(n\in\mathbb{Z}\)

Uma parametrização de \(\ell_{\alpha}\) é dada por: $$\begin{array}{ccll}
\ell_{\alpha}: & ]0\,,\pi[ & \longrightarrow & \mathbb{S}^{2}\\ & \varphi & \mapsto & \left(r\cos\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\, r\sen\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\, r\cos\varphi\right)
\end{array}\,,$$ com $$\theta_\alpha(\varphi)=\theta_{P}+\tg\alpha\left[\ln\left(\cotg\frac{\varphi}{2}\right)-
\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\right]\,.$$ Como já observámos, esta curva pode ser estendida continuamente a \([0\,,\pi]\), logo o comprimento da curva \(\ell_{\alpha}\) é dado pelo integral \(\int_{0}^{\pi}\Vert\ell_{\alpha}^{\prime}(\varphi)\Vert\, d\varphi\).

Temos que: $$\begin{array}{rccl}
\ell_{\alpha}^{\prime}(\varphi) & = & & r\,\theta'_\alpha\left(\varphi\right)\left(-\sen\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,\cos\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,0\right)\\ & & + & r\left(\cos\varphi\cos\left(\theta_\alpha\left(\varphi\right)\right)\,,\,\cos\varphi\sen\left(\theta_\alpha\left(\varphi\right)\right)\,,\,-\sen\varphi\right)\,.
\end{array}$$ Calculando \(\Vert\ell_{\alpha}^{\prime}(\varphi)\Vert\) obtém-se $$\Vert\ell_{\alpha}^{\prime}(\varphi)\Vert=r\sqrt{\left[\theta'_\alpha(\varphi)\right]^{2}\sen^{2}\varphi+1}\,.$$ Como \(\theta'_\alpha\left(\varphi\right)=-\frac{\tg\alpha}{\sen\varphi}\), vem que $$\Vert\ell_{\alpha}^{\prime}(\varphi)\Vert=r\sqrt{\tg{}^{2}\alpha+1}=\frac{r}{\left|\cos\alpha\right|}\,.$$

A vermelho está representada uma curva loxodrómica cujo traço tem a forma de espiral. A azul está assinalado o caminho mais curto entre os dois pontos (menor arco de círculo máximo que os contém).

Logo, se \(\alpha\neq\frac{\pi}{2}+n\pi\), com \(n\in\mathbb{Z}\), o comprimento da curva \(\ell_{\alpha}\) é $$\int_{0}^{\pi}\frac{r}{\left|\cos\alpha\right|}\,d\varphi=\frac{\pi}{\left|\cos\alpha\right|}r.$$

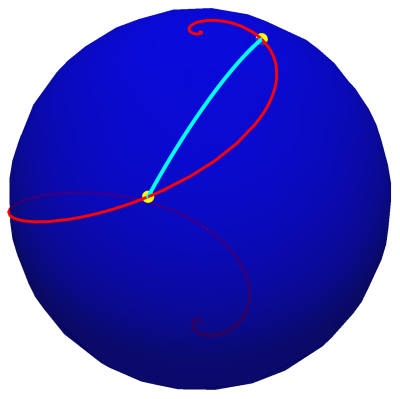
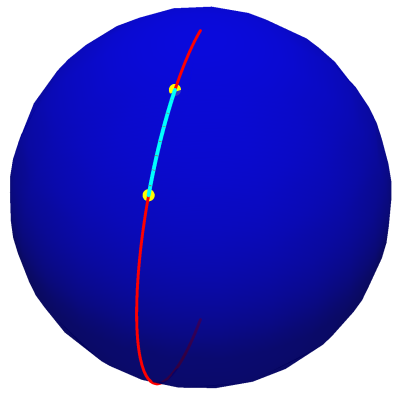
Quando \(\alpha=0\), o traço da curva coincide com um meridiano. Logo, o seu comprimento é igual a metade do perímetro de uma circunferência de raio \(r\), \(\pi r\).

Note-se ainda que, nos restantes casos (\(\alpha\neq\frac{\pi}{2}+n\pi\)), apesar do traço da curva loxodrómica assumir a forma de uma "espiral infinita'', o seu comprimento é finito.

Se quisermos calcular o comprimento do arco da curva \(\ell_{\alpha}\) entre dois pontos quaisquer da curva \(Q\,\left(r,\theta_{Q},\varphi_{Q}\right)\) e \(R\,\left(r,\theta_{R},\varphi_{R}\right)\) temos de determinar o valor de \(\left|\int_{\varphi_{R}}^{\varphi_{Q}}\frac{r}{\left|\cos\alpha\right|}\, d\varphi\right|\), que é igual a \(\frac{\left|\varphi_{Q}-\varphi_{R}\right|}{\left|\cos\alpha\right|}r\).

Pode-se mostrar que este comprimento é superior ou igual ao comprimento do menor arco de círculo máximo definido pelos dois pontos, ou seja, um percurso segundo a curva loxodrómica não é, em geral, o caminho mais curto entre dois pontos.

Curva loxodrómica que coincide com um meridiano. Neste caso, o arco da curva entre dois pontos corresponde ao caminho mais curto entre eles.