-
r
é a distância de P a O;
-
θ é o ângulo que a projecção de \(\overrightarrow{OP}\)
no plano z = 0 faz com o semi-eixo positivo Ox,
variando entre 0 e 2π rad
-
\(\varphi\)
é o ângulo que \(\overrightarrow{OP}\) faz com o semi-eixo
positivo Oz, variando entre 0 e π rad.
Tendo
em conta que P se situa numa esfera com centro em O e raio r, designaremos θ por longitude e \(\varphi\) por colatitude. Na superfície
terrestre, o conjunto dos pontos com a mesma longitude é um meridiano
e o conjunto dos pontos com a mesma colatitude é um paralelo,
sendo a linha do Equador o conjunto dos pontos com colatitude
\(\frac{\pi}{2}\) rad.
Assim,
a relação entre as coordenadas cartesianas \(\left(x,y,z\right)\)
e as coordenadas esféricas \(\left(r,\theta,\varphi\right)\) de
um ponto da esfera de raio r e centro na origem do referencial é dada por:
\(\begin{cases}
x=r\cos\theta\sen\varphi\\
y=r\sen\theta\sen\varphi\\
z=r\cos\varphi
\end{cases}\), \(\theta\in[0\,,2\pi]\) e \(\varphi\in[0\,,\pi]\).
|
|
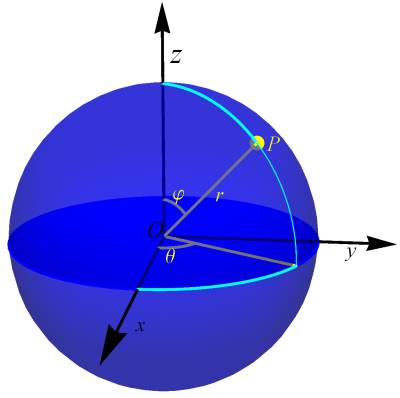
Coordenadas
esféricas
\(\left(r,\theta,\varphi\right)\) de um ponto P.
|
|
