|
|
 |
 |
|
 |
|
|
|
 |
|
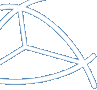
Ao compor duas das 24 rotações,
não descobrimos nenhuma nova simetria, porque o
resultado é ainda uma rotação - embora
nem sempre seja fácil de visualizar:
|
 fig1 fig1
|
por exemplo,
vê-se logo, que se efectuarmos duas rotações
em torno de uma mesma recta r, a primeira de 1/4 de volta
e a segunda de meia volta, obteremos uma rotação
de 3/4 de volta, sempre em torno da mesma recta; |
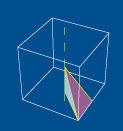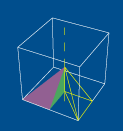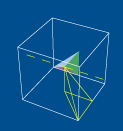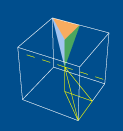 fig2 fig2
|
enquanto,
por exemplo, é bem mais complicado observar que,
compondo uma rotação de 1/4 de volta em torno
do eixo dos zz com uma rotação de meia volta
em torno do eixo dos yy (ver figura 2), se obtém
uma rotação de meia volta em torno da recta
t (ver figura 3).
|
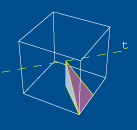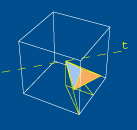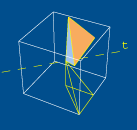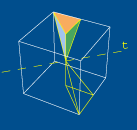 fig3 fig3
|
Entre as restantes 24 simetrias
encontram-se as nove simetrias de reflexão relativas
aos nove planos de onde partimos, e mais 15 que são
um pouco mais complicadas de descrever explicitamente,
mas que podem ser facilmente encaradas como transformações
compostas, ou seja, obtidas efectuando sucessivamente
duas transformações e considerando a transformação
resultante.
|
 fig4 fig4
|
Na verdade, se compusermos
uma das nove reflexões (atrás descritas)
com cada uma das 24 rotações, encontraremos
todas as restantes 24 simetrias do cubo que não
são rotações, entre as quais se encontram
também essas nove reflexões. Na figura ao
lado é possível observar, por exemplo, para
onde se desloca a pirâmide de referência,
compondo a reflexão em relação ao
plano XOY com a rotação de meia volta em
torno do eixo dos zz.
|
Texto adaptado de um
texto original (italiano) de Cristina Vezzani
|
 |

|
|
|
|
|