|
Seja
\(\ell_{\alpha}\) uma curva loxodrómica cujo ângulo de intersecção
com os meridianos é \(\alpha\in\left[-\frac{\pi}{2},\,\frac{\pi}{2}\right]\)
e que passa num ponto P com coordenadas
esféricas \(\left(r,\theta_{P},\varphi_{P}\right)\,,\)
com \(\theta_{P}\in[0\,,2\pi]\) e \(\varphi_{P}\in\ ]0\,,\pi[\).
A parametrização
da curva loxodrómica \(\ell_{\alpha}\) pode ser definida por:
-
Se
\(\alpha=\pm\frac{\pi}{2}\),
$$\begin{array}{ccll}
\ell_{\alpha}: & [0\,,2\pi] & \longrightarrow &
\mathbb{S}^{2}\\
& \theta & \mapsto & \left(r\cos\theta\sen\left(\varphi_{P}\right)\,,\,
r\sen\theta\sen\left(\varphi_{P}\right)\,,\, r\cos\left(\varphi_{P}\right)\right)&.
\end{array}$$ Neste
caso, o seu traço corresponde a um paralelo com a mesma
latitude que P; em particular,
se \(\varphi_{P}=\frac{\pi}{2}\), \(\ell_{\alpha}\) dá-nos
uma parametrização da linha do Equador.
-
Se
\(\alpha\in\left]-\frac{\pi}{2},\,\frac{\pi}{2}\right[\),
$$\begin{array}{ccll}
\ell_{\alpha}: & ]0\,,\pi[ & \longrightarrow &
\mathbb{S}^{2}\\
& \varphi & \mapsto & \left(r\cos\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,
r\sen\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,
r\cos\varphi\right)&,
\end{array}$$
com \(\theta_\alpha(\varphi)=\theta_{P}+\tg\alpha\left[\ln\left(\cotg\frac{\varphi}{2}\right)-\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\right]\).
|
|
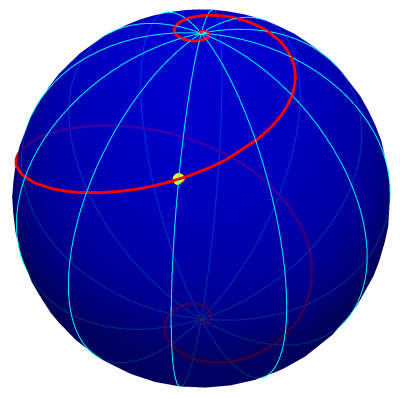
Curva loxodrómica cujo traço tem a forma
de espiral.
|
|