|
Na
época dos Descobrimentos, o matemático Pedro Nunes
descobriu que as rotas de navegação que mantêm o percurso
de um navio num rumo constante, intersectando todos os meridianos
segundo o mesmo ângulo, determinam um tipo de curva, que ficou
conhecida por curva loxodrómica
Desde
essa época que se sabe que um percurso mantendo um ângulo
constante em relação aos meridianos não é, em geral, o caminho
mais curto, pois não é um arco de círculo máximo (curva na
esfera que minimiza a distância entre dois pontos - para mais
pormenores pode consultar a página do Atractor dedicada à
Geometria Esférica).
Se os descobridores portugueses quisessem seguir um círculo
máximo, de forma a obter o caminho mais curto entre dois locais
do planeta, teriam que estar continuamente a avaliar e a modificar
o ângulo de navegação, tarefa essa que era impraticável em
alto mar naquela época. Portanto, a maneira mais simples
de navegar era mantendo o ângulo constante. (Randles, 1989
[1])
*Neste
trabalho, quando daí não resultar qualquer ambiguidade, identificaremos
a curva com o seu traço,
ou seja, frequentemente não distinguiremos duas curvas com o mesmo traço. |
|
|
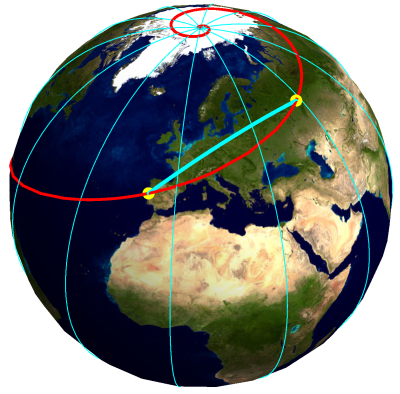
A vermelho está representada
uma curva loxodrómica que passa por dois pontos
e a azul o menor arco de círculo máximo definido
por esses pontos (caminho mais curto).
|
|