Inversão

É natural chamar inversão à função que a cada número real maior que zero associa o seu inverso . Esta função envia 1 em 1: 1 é ponto fixo para a inversão. A inversão envia a semirecta representando os números maiores que zero sobre si própria, trocando a semirecta vermelha com o segmento azul:

O produto das distâncias à origem de qualquer ponto e do seu inverso é (sempre) 1.

Se quisermos estender esta noção ao plano ou ao espaço, podemos definir uma inversão de centro num ponto O, aplicando a cada semirecta de origem O a ideia descrita acima. O inverso de um ponto P diferente de O será o ponto P' da semirecta OP, tal que .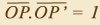

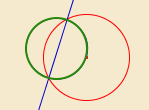
No plano, todos os pontos da circunferência unitária centrada em O ficam fixos por esta transformação: essa circunferência diz-se a circunferência de inversão. A inversão troca as regiões azul e violeta:

Analogamente, teremos no espaço uma superfície esférica de inversão de raio 1 e centro O, constituída por pontos fixos para a inversão.

N.B. - É possível considerar, mais geralmente, circunferências de inversão de raios diferentes de 1. Se C é uma circunferência de centro O e raio r, o inverso de um ponto P diferente de O, relativamente a C, será o ponto P' da semirecta OP, tal que . (Analogamente se define a inversão no espaço, relativamente a uma superfície esférica qualquer.)

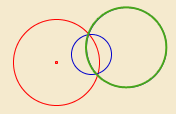
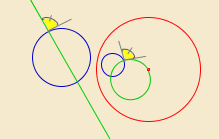
Algumas propriedades da inversão no plano

Qualquer recta que não passe pelo centro de inversão O é enviada numa circunferência que passa pelo centro de inversão (o único ponto dessa circunferência que não é inverso de um ponto da recta é O). Caso a recta passe por O, O determina na recta duas semirectas abertas (de extremo O). Cada uma dessas semirectas é enviada pela inversão nela própria, sendo trocada a parte que está dentro da circunferência com a que está fora.
Qualquer circunferência que não passe pelo centro de inversão O é enviada sobre uma circunferência. No caso de a circunferência passar por O, os seus pontos diferentes de O terão como inversos (todos) os pontos de uma recta.
A inversão conserva ângulos. Em particular, a inversão conserva tangência e ortogonalidade. Há planos de incluir mais tarde no site as demonstrações desta e das outras propriedades da inversão acima mencionadas. Para quem é familiar com as propriedades dos números complexos e das funções analíticas, algumas das propriedades deduzem-se de maneira muito simples e elegante de uma definição alternativa da inversão.