Inversão

(no plano complexo C)

Se tivermos presentes algumas propriedades elementares dos números complexos, podemos facilmente dar uma descrição alternativa da inversão geométrica atrás definida e deduzir algumas das propriedades enunciadas.

Um complexo fica determinado pelo seu módulo (distância à origem) e pelo seu argumento (ângulo da semirecta real positiva com a semirecta emitida da origem e determinada pelo complexo).

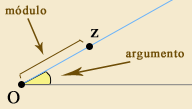
E não é dificil concluir que o módulo do produto de dois complexos é igual ao produto dos módulos e que o argumento do produto é a soma dos argumentos.

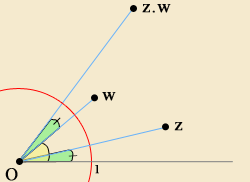
Destas propriedades resulta imediatamente que, dado um complexo não nulo z:

o módulo do seu inverso (no sentido da multiplicação de complexos, isto é, o número que multiplicado por z dá 1) é igual ao inverso do seu módulo: o produto das distâncias à origem dos pontos correspondentes é 1. a soma dos argumentos do complexo e do seu inverso (na mesma acepção) é 0 (argumento de 1).

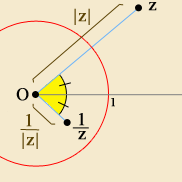Se compararmos esta inversão para a multiplicação com a inversão geométrica atrás definida no plano, vemos que não coincidem. Mas os inversos de um mesmo ponto, nas duas acepções, são simétricos um do outro relativamente à recta real no plano complexo. Ora esta simetria corresponde à função que troca o sinal à parte imaginária de um complexo, isto é, corresponde à passagem ao conjugado.

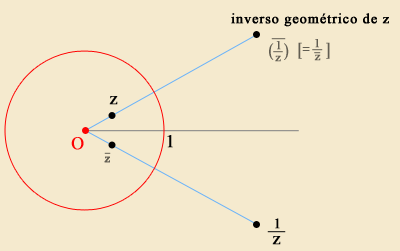
Portanto, a inversão geométrica anteriormente considerada pode ser descrita em termos dos números complexos pela função ou .

Ora, obviamente que a passagem ao conjugado, traduzida geometricamente por uma reflexão, conserva ângulos (além de trocar a orientação). E resulta de propriedades gerais das funções analíticas, que a função também conserva ângulos (além de conservar a orientação). Portanto, a inversão geométrica, como composta das duas, também conserva ângulos (além de trocar a orientação).