Inversor de Peaucellier

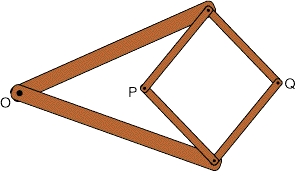
Peaucellier foi um oficial do exército francês que apresentou em 1867 a solução para um problema mecânico exigido pelo desenvolvimento da tecnologia: a transformação de um movimento circular num movimento rectilíneo. James Watt, o inventor da máquina a vapor, tinha apresentado uma solução aproximada, usando um outro mecanismo que traçava uma lemniscata de Bernoulli. Parte desta curva é aproximadamente linear, e essa era a solução aproximada de Watt. O mecanismo de Peaucellier fornece a solução exacta para o problema. É constituído por seis hastes (ver figura).

Duas destas hastes, iguais, têm como extremo comum um pivot fixo, O. As outras quatro hastes formam um losango, em que dois vértices opostos são articulados nas extremidades livres das duas hastes ligadas a O. Quando o ponto P descreve uma determinada curva c, o ponto Q descreve uma curva c', "transformada" da primeira. Em particular, se P é obrigado a descrever uma circunferência passando pelo pivot O, então Q descreve uma recta.

Por meio de um applet JavaSketchpad, iremos fazer uma modelação do mecanismo e verificar precisamente essa transformação de um movimento circular num movimento rectilíneo.

Modelação do Inversor de Peaucellier em JavaSketchpad

No applet Java seguinte, o conjunto das hastes verdes e amarelas forma o inversor de Peaucellier. Podemos alterar o comprimento das hastes arrastando as suas extremidades no parte superior esquerda da figura -- teremos naturalmente que manter sempre o comprimento da haste verde superior ao comprimento da haste amarela.

Arrastando o ponto P, ele desloca-se ao longo da circunferência azul (centro G e raio dado pelo segmento azul), enquanto o seu "transformado" Q, pelo mecanismo de Peaucellier, descreve a circunferência vermelha. Podemos animar o ponto P sobre a circunferência azul clicando no botão animate. Para interromper a animação, basta clicar de novo sobre o botão animate.

Se arrastarmos o ponto G, centro da circunferência azul, até fazer passar esta circunferência pelo pivot O, a circunferência vermelha parece transformar-se numa recta. Se animarmos, para esta posição da circunferência azul, o ponto P, verificaremos que o ponto Q descreve a recta vermelha, embora quando o ponto P está próximo de O o mecanismo desapareça! Na realidade, dado que as hastes têm comprimento limitado, o ponto P apenas pode descrever um arco de circunferência (não contendo O) e não "toda a circunferência". O ponto Q, portanto, apenas irá descrever um segmento de recta, e não "toda a recta". Podemos também, para transformar a circunferência azul numa que passe pelo pivot O, clicar no botão circ ---> recta.