Demonstração

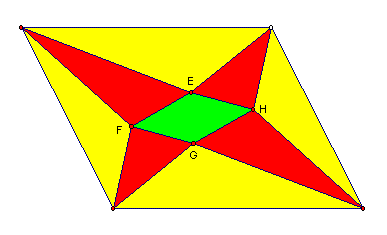
Vamos considerar dois casos distintos.

1ºCaso

Neste caso, a área do paralelogramo de Morley pode ser obtida subtraindo à área do paralelogramo inicial as áreas dos triângulos a amarelo e a vermelho. Supondo que os lados do paralelogramo inicial medem $a=\overline{AD}$ e $b=\overline{AB}$ e formam um ângulo de amplitude , a sua área é $ab\sin \alpha$ . Em relação à área dos triângulos, esta é dada por metade do produto do comprimento de dois dos seus lados pelo seno do ângulo adjacente a esses lados.

Por exemplo, para calcular a área do triângulo $\left[ ADE\right]$ precisamos de saber a medida dos lados $\left[ AE\right]$ e $\left[ DE\right]$ e a amplitude do ângulo $\measuredangle AED$ . Utilizando a lei dos senos, temos:

MATH

Analogamente, temos:

Notemos agora que os triângulos $\left[ ADE\right]$ e $\left[ CBG\right]$ são congruentes, assim como os triângulos $\left[ ABF\right]$ e $\left[ CDH\right]$ . Logo, a soma das áreas dos triângulos amarelos é:

Considerando agora os triângulos a vermelho e usando o facto de os triângulos $\left[ EAF\right]$ e $\left[ GCH\right]$ serem congruentes, assim como os triângulos $\left[ FBG\right]$ e $\left[ HDE\right]$ , temos:

Utilizando a fórmula deduzida na demonstração trigonométrica do teorema de Morley, podemos então concluir que a soma das áreas dos triângulos vermelhos é:

MATH

(ou seja, a soma das áreas dos triângulos vermelhos é exactamente um terço da área do paralelogramo ).

Podemos agora calcular a área do paralelogramo :

2º Caso

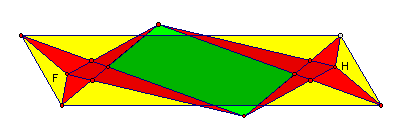
Neste caso, a soma das áreas dos triângulos $\left[ ADE\right]$ , $\left[ CBG\right]$ , $\left[ ABF\right]$ , $\left[ CDH\right]$ , $\left[ EAF\right]$ , $\left[ GCH\right]$ , $\left[ FBG\right]$ e $\left[ HDE\right]$ excede a área do paralelogramo e esse excesso é exactamente a área do paralelogramo . Além disso, facilmente se conclui que os valores obtidos no caso anterior para as áreas dos triângulos mencionados permanecem válidos. Logo, vem:

Em ambos os casos temos:

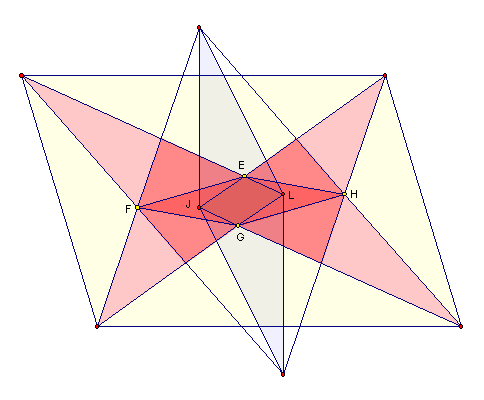
Relativamente à área do paralelogramo , notemos em primeiro lugar que os triângulos $\left[ EAF\right]$ e $\left[ LAK\right]$ são semelhantes. De facto, temos:

MATH

Analogamente, os triângulos $\left[ EDH\right]$ e $\left[ JDK\right]$ também são semelhantes, uma vez que temos:

MATH

Usando a congruência entre os triângulos $\left[ BGF\right]$ e $\left[ DEH\right]$ e a semelhança entre os triângulos $\left[ EAF\right]$ e $\left[ LAK\right]$ e os triângulos $\left[ EDH\right]$ e $\left[ JDK\right]$ , vem:

$E\widehat{F}G$ =

$=J\widehat{K}L$

MATH

Logo, vem:

Conclusão:

Note-se que a razão entre as áreas (supondo ambas não nulas) é:

MATH

, com .

Logo, temos que , ou seja, o paralelogramo tem uma área que é sempre maior que o dobro da área do paralelogramo e nunca superior ao seu triplo, o qual é atingido quando . Notemos ainda que, como , e , os paralelogramos e só são semelhantes quando , ou seja, quando . Quando tal acontece, a razão de semelhança é , pelo que a razão entre as áreas é $(\sqrt{3})^{2}=3$ , conforme foi referido.