Cissóide é o nome dado por Geminus (séc. I a.C.), nos seus comentários ao livro de Arquimedes "Sobre a Esfera e o Cilindro". Geminus atribui a Diocles a invenção desta curva como contribuição para a resolução do problema clássico da Duplicação do Cubo. Com esta curva, é possível determinar dois meios proporcionais entre dois segmentos dados, e esta determinação, como foi demonstrado por Hipócrates de Quios (c.470-c.410 a.C.), é suficiente para obter a duplicação do cubo. A estrofóide foi estudada por vários matemáticos no século XVII (Isac Barrow, Torricelli e Roberval). O mecanismo, em madeira, quando desmontado consiste em quatro peças:
Este mecanismo pode traçar a cissóide de Diocles (c. 240 - mc. 180 a. C.) e a estrofóide recta.
• Uma base rectangular ABCD, sobre a qual se coloca uma folha de papel A3 onde será traçada a cissóide (ou a estrofóide).
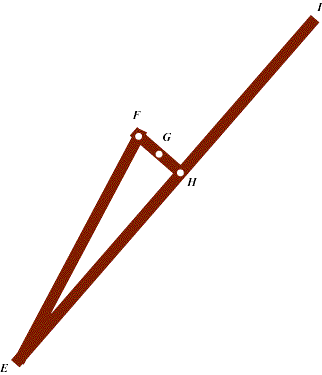
• Uma peça EFGHI, com duas posições (G e H) onde é possível colocar um lápis ou uma caneta.
• Uma haste JK que serve para conduzir a peça anterior (ver mais à frente).
• Uma pequena calha giratória que vai obrigar a peça EFGHI a rodar durante o seu deslocamento (ver mais à frente)

 |
 |
|||
Para montar o mecanismo:
• coloca-se a haste JK no topo da base;
• enfia-se um pino que existe na calha giratória no furo P da base;
• utiliza-se o pino L, que existe na haste, para fixar a peca EFGHI a esta, servindo-nos para isso do furo F, tendo o cuidado de fazer passar a haste EF na calha giratória.
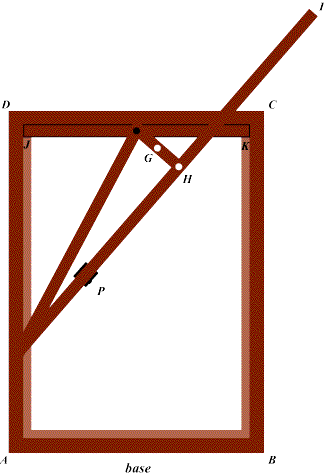
Depois de montado, o mecanismo apresenta-se como a figura seguinte (à esquerda). Colocado o lápis na posição G, quando fazemos deslizar a haste JK de cima para baixo, a calha P obriga a peça EFGHI a rodar em torno do pino situado a meio da haste JK e vai sendo traçada uma cissóide. No caso de colocarmos o lápis no furo H, a curva desenhada é a estrofóide recta.
 |
||
 |
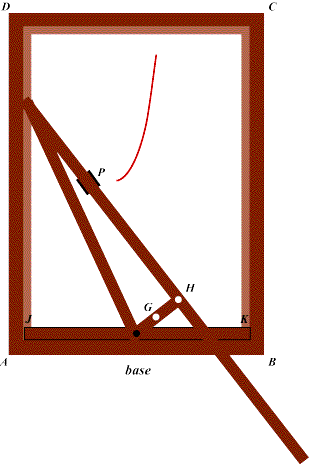
A curva desenhada na figura da direita corresponde à parte da cissóide que é tracada pelo mecanismo quando a haste JK percorre todo o percurso possível de cima para baixo (até ser detida pela calha giratória). Para obter a outra parte da curva, simétrica em relação a um eixo de simetria passando pelo ponto P, há que montar agora o mecanismo com a haste JK no extremo inferior da base, como se vê na figura seguinte. E depois retomar o mesmo processo, agora fazendo descolar a haste JK, e a peça EFGHI, de baixo para cima.
 |
Se possui o programa Sketchpad, poderá ver aqui uma animação esquemática deste mecanismo.
Notas:
a) Conforme o lápis é colocado no ponto G ou no ponto H assim se obtém uma cissóide ou uma estrofóide. A estrofóide não se pode obter completamente devido movimento da haste JK ser interrompido pela calha giratória.
b) O movimento da peça EFGHI pode ser obtido ou movendo a haste JK ou utilizando o próprio lápis para fazer deslocar o mecanismo.
c) As folhas A3 para traçar cissóides (resp. estrofóides) têm no verso informações sobre a respectiva curva.
Bibliografia:
• Macchine matematiche e altri oggeti, Maria G. Bartolini Bussi e Pasquale Quattrocchi, Nucleo di Ricerca in Storia e Diddattica della Matematica. Universita degli Studi di Modena.