PARA
SABER MAIS...
Fixado
um ponto C da esfera, denominado por origem da projecção, a projecção
estereográfica de um ponto P≠C da esfera estará no plano tangente à esfera no ponto antípoda
(ponto diametralmente oposto) de C. Esse
plano é designado por plano de projecção. A projecção de P resulta da intersecção da semi-recta CP com o plano de projecção.
A
projecção estereográfica aqui definida tem como origem da projecção
o Pólo Sul e, portanto, o plano de projecção é o plano tangente à
esfera no Pólo Norte. Note-se que a projecção do ponto coincidente
com o Pólo Sul não está definida.
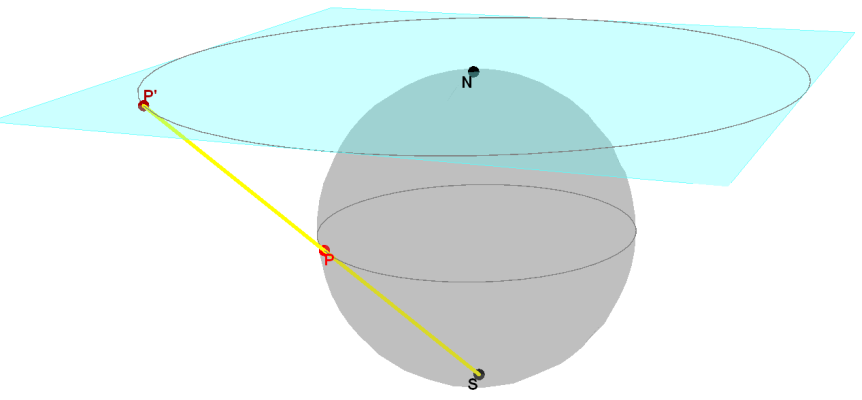
Esquema da Projecção
Estereográfica com Origem no Pólo Sul.
|
|
Dado
um ponto P na esfera com coordenadas esféricas \(\left(r,\theta,\varphi\right)\)
e P′ a projecção estereográfica
de P definida acima, então as coordenadas de P′
são dadas por \(2r\tg\left(\frac{\varphi}{2}\right)\left(\cos\theta\,,\,\sen\theta\right)\).
Contudo,
para uma melhor visualização dos países no mapa da projecção
estereográfica escolhida, consideramos o plano do mapa obtido
pela rotação do plano de projecção de amplitude \(\frac{\pi}{2}\)
no sentido negativo e centro na origem do referencial.
Assim,
a projecção estereográfica é a função \(\mathcal{E}\) da esfera
de raio r no plano induzida por:
$$\begin{array}{ccll}
\mathcal{E}: & \mathbb{R}\,\times\,]0\,,\pi[ & \longrightarrow
&\mathbb{R}^{2}\\& \left(\theta,\varphi\right) &
\mapsto & 2r\tg\frac{\varphi}{2}\left(\cos\left(\theta-\frac{\pi}{2}\right)\,,\,\sen\left(\theta-\frac{\pi}{2}\right)\right)
\end{array}\,.$$
|
|
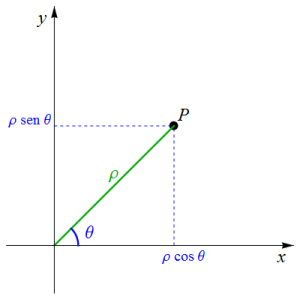
Um ponto qualquer
do plano \(\mathbb{R}^{2}\) pode ser determinado sabendo
as suas coordenadas polares: \(\left(\rho,\theta\right)\),
onde \(\rho\) é a distância do ponto à origem O do referencial
e θ é a amplitude do ângulo que o vector \(\overrightarrow{OP}\)
faz com o semi-eixo positivo das abcissas. Assim, as
suas coordenadas cartesianas são dadas por \(\rho\left(\cos\theta\,,\,\sen\theta\right)\).
|
|
| 1.
Recordemos que, se \(\alpha\neq\frac{\pi}{2}+n\pi\),
\(n\in\mathbb{Z}\), uma parametrização
de \(\ell_{\alpha}\) que passa num ponto
P com coordenadas esféricas \(\left(r,\theta_{P},\varphi_{P}\right)\)
é dada por: $$\ell_{\alpha}\left(\varphi\right)=\left(r\cos\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,r\sen\left(\theta_\alpha\left(\varphi\right)\right)\sen\varphi\,,\,r\cos\varphi\right)\,,$$
com \(\varphi\in\,]0\,,\pi[\) e \(\theta_\alpha(\varphi)=\theta_{P}+\tg\alpha\left[\ln\left(\cotg\frac{\varphi}{2}\right)-\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\right]\,.\)
Assim,
a projecção da curva loxodrómica é a função \(\mathcal{E}\circ\ell_{\alpha}\)
definida por: $$\begin{array}{ccll}
\mathcal{E\circ}\ell_{\alpha}: & ]0\,,\pi[ & \longrightarrow
& \mathbb{R}^{2}\\ & \varphi & \mapsto & 2r\tg\frac{\varphi}{2}\left(\cos\left(\theta_\alpha\left(\varphi\right)-\frac{\pi}{2}\right)\,,\,\sen\left(\theta_\alpha\left(\varphi\right)-\frac{\pi}{2}\right)\right)
\end{array}\,.$$
Supondo
adicionalmente que \(\alpha\neq n\pi,\, n\in\mathbb{Z}\), e
definindo \(\varphi\) em função de \(\theta\), vem que \(\varphi_\alpha\left(\theta\right)=2\arccotg\left(e^{\frac{\theta-k}{\tg\alpha}}\right)\),
com \(k=\theta_{P}-\tg\alpha\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\).
Logo,
podemos reparametrizar a projecção estereográfica da curva da
seguinte forma: $$\begin{array}{ccll}
\mathcal{E\circ}\ell_{\alpha}\circ\varphi_\alpha: & \mathbb{R}
& \longrightarrow & \mathbb{R}^{2}\\ & \theta &
\mapsto & 2r\, e^{\frac{k-\theta}{\tg\alpha}}\left(\cos\left(\theta-\frac{\pi}{2}\right)\,,\,\sen\left(\theta-\frac{\pi}{2}\right)\right)
\end{array}\,,$$ com \(k=\theta_{P}-\tg\alpha\ln\left(\cotg\frac{\varphi_{P}}{2}\right)\).
O
traço de uma curva assim definida é uma espiral.
|
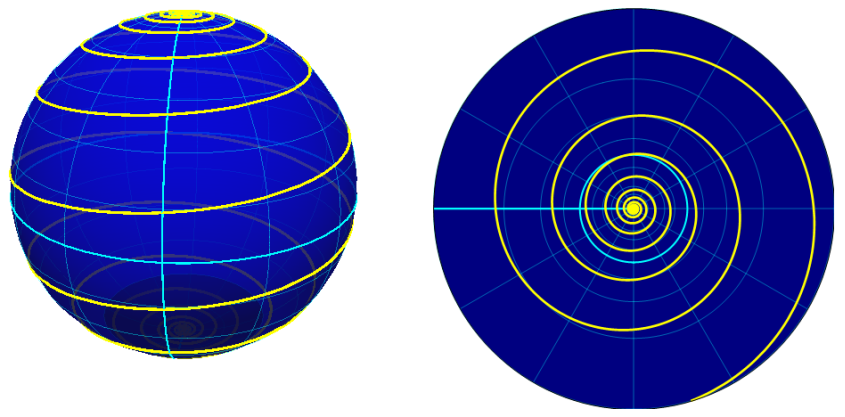
Curva loxodrómica
projectada no plano pela Projecção Estereográfica.
A latitude varia entre -60º e 90º.
|
|
2.
Se \(\alpha=\frac{\pi}{2}+n\pi\), para algum \(n\in\mathbb{Z}\),
uma
parametrização de \(\ell_{\alpha}\) que passa num ponto P com coordenadas esféricas \(\left(r,\theta_{P},\varphi_{P}\right)\)
é dada por:
\(\ell_{\alpha}\left(\theta\right)=\left(r\cos\left(\theta\right)\sen\left(\varphi_{P}\right)\,,\,
r\sen\left(\theta\right)\sen\left(\varphi_{P}\right)\,,\, r\cos\left(\varphi_{P}\right)\right)\,,\)
com \(\theta\in\,[0,2\pi]\),
cujo
traço na esfera é um paralelo.
Neste
caso, a projecção da curva loxodrómica é a função \(\mathcal{E}\circ\ell_{\alpha}\)
definida por: $$\begin{array}{ccll}\mathcal{E\circ}\ell_{\alpha}:
& [0\,,2\pi] & \longrightarrow & \mathbb{R}^{2}\\&
\theta & \mapsto & 2r\tg\frac{\varphi_{P}}{2}\left(\cos\left(\theta-\frac{\pi}{2}\right)\,,\,\sen\left(\theta-\frac{\pi}{2}\right)\right)\;.
\end{array}$$ Como
\(2r\tg\frac{\varphi_{P}}{2}\) é uma constante positiva, a função
define uma circunferência no plano de raio \(2r\tg\frac{\varphi_{P}}{2}\)
e centro na origem do referencial.
|
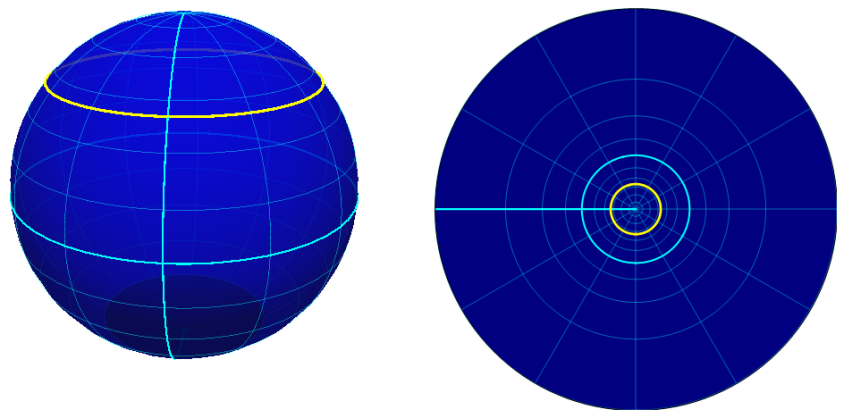
Curva loxodrómica
perpendicular aos meridianos projectada no plano usando
a Projecção Estereográfica.
A latitude varia entre -60º
e 90º.
|
|
3.
Se \(\alpha=n\pi\), para algum \(n\in\mathbb{Z}\),
uma
parametrização de \(\ell_{\alpha}\) que passa num ponto P com coordenadas esféricas \(\left(r,\theta_{P},\varphi_{P}\right)\)
é dada por:
\(\ell_{\alpha}\left(\varphi\right)=\left(r\cos\left(\theta_{P}\right)\sen\varphi\,,\,r\sen\left(\theta_{P}\right)\sen\varphi\,,\,
r\cos\varphi\right)\,\), com \(\varphi\in\,]0,\pi[\),
cujo
traço na esfera é um meridiano.
Neste
caso, a projecção da curva loxodrómica é a função \(\mathcal{E}\circ\ell_{\alpha}\)
definida por: $$\begin{array}{ccll}\mathcal{E\circ}\ell_{\alpha}:
& ]0\,,\pi[ & \longrightarrow & \mathbb{R}^{2}\\&
\varphi & \mapsto & 2r\tg\frac{\varphi}{2}\left(\cos\left(\theta_{P}-\frac{\pi}{2}\right)\,,\,\sen\left(\theta_{P}-\frac{\pi}{2}\right)\right)\;,
\end{array}$$ uma
semi-recta com origem em \((0,0)\) e declive \(\tg\left(\theta_{P}-\frac{\pi}{2}\right)\).
|
|



