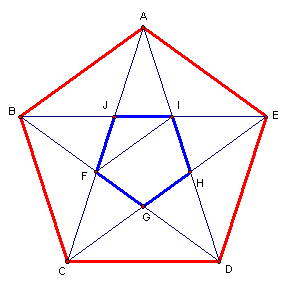
Pentágono regular

Seja  um pentágono regular,
um pentágono regular, 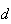 a medida da sua diagonal e
a medida da sua diagonal e 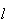 a medida do seu lado. Supondo que
a medida do seu lado. Supondo que 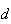 e
e 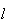 são comensuráveis, temos
são comensuráveis, temos 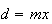 e
e 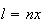 ,
onde
,
onde 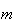 e
e 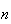 são inteiros positivos e
são inteiros positivos e 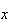 é uma medida comum à diagonal e ao lado do pentágono.
é uma medida comum à diagonal e ao lado do pentágono.
Sejam 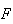 ,
,
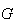 ,
,
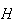 ,
,
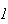 e
e 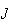 os pontos de intersecção das diagonais. Construindo
a circunferência que circunscreve o pentágono, notemos que os pontos
os pontos de intersecção das diagonais. Construindo
a circunferência que circunscreve o pentágono, notemos que os pontos
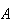 ,
,
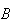 ,
,
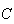 ,
,
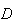 e
e 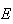 dividem esta em arcos de igual amplitude, dada por
dividem esta em arcos de igual amplitude, dada por 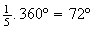 .
Considerando, por exemplo, o triângulo
.
Considerando, por exemplo, o triângulo ![$\left[ FBC\right] $](graphics/pentagono2__22.gif) ,
temos que
,
temos que 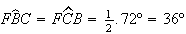 (ângulos inscritos numa circunferência têm como amplitude metade
do valor do respectivo arco), logo ele é isósceles. Analogamente,
os triângulos
(ângulos inscritos numa circunferência têm como amplitude metade
do valor do respectivo arco), logo ele é isósceles. Analogamente,
os triângulos ![$\left[ GCD\right] $](graphics/pentagono2__24.gif) ,
,
![$\left[ HDE\right] $](graphics/pentagono2__25.gif) ,
,
![$\left[ IEA\right] $](graphics/pentagono2__26.gif) e
e ![$\left[ JAB\right] $](graphics/pentagono2__27.gif) também são isósceles. Além disso, são todos congruentes
entre si, pois têm um lado e os ângulos adjacentes iguais. Logo,
também são isósceles. Além disso, são todos congruentes
entre si, pois têm um lado e os ângulos adjacentes iguais. Logo, 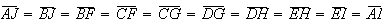 e, como
e, como 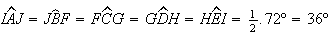 ,
os triângulos
,
os triângulos ![$\left[ IAJ\right] $](graphics/pentagono2__30.gif) ,
,
![$\left[ JBF\right] $](graphics/pentagono2__31.gif) ,
,
![$\left[ FCG\right] $](graphics/pentagono2__32.gif) ,
,
![$\left[ GDH\right] $](graphics/pentagono2__33.gif) e
e ![$\left[ HEI\right] $](graphics/pentagono2__34.gif) também são isósceles e congruentes entre si. Temos então
que
também são isósceles e congruentes entre si. Temos então
que 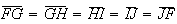 e que
e que 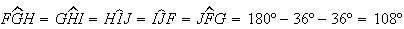 ,
pelo que
,
pelo que 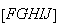 é um pentágono regular.
é um pentágono regular.
Como 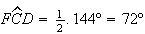 e
e 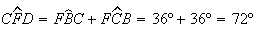 ,
vem que
,
vem que ![$\left[ FCD\right] $](graphics/pentagono2__40.gif) é isósceles, com
é isósceles, com 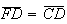 .
Analogamente,
.
Analogamente, ![$\left[ BCG\right] $](graphics/pentagono2__42.gif) também é isósceles, com
também é isósceles, com 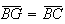 .
Além disso, como
.
Além disso, como 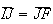 ,
temos que
,
temos que ![$\left[ IJF\right] $](graphics/pentagono2__45.gif) é isósceles e
é isósceles e 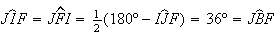 ,
pelo que
,
pelo que ![$\left[ BFI\right] $](graphics/pentagono2__47.gif) também é isósceles, com
também é isósceles, com 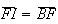 .
Designando por
.
Designando por 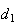 a medida da diagonal de
a medida da diagonal de 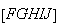 e por
e por 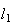 a medida do seu lado, temos:
a medida do seu lado, temos:
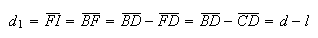
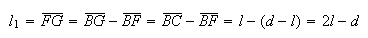
Como 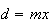 e
e 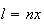 ,
temos:
,
temos:
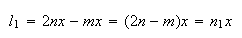
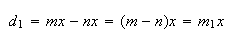
onde 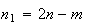 e
e 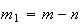 são dois números inteiros positivos, com
são dois números inteiros positivos, com 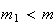 .
Procedendo da mesma forma com o pentágono
.
Procedendo da mesma forma com o pentágono 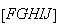 ,
vamos obter um novo pentágono regular cuja diagonal é
,
vamos obter um novo pentágono regular cuja diagonal é 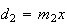 e cujo lado é
e cujo lado é 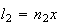 ,
sendo que
,
sendo que 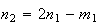 e
e 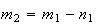 são dois números inteiros positivos, com
são dois números inteiros positivos, com 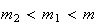 .
.
Uma vez que podemos continuar indefinidamente a construir novos pentágonos regulares, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
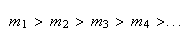
tal que
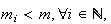 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que 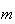 (de facto, existem exactamente
(de facto, existem exactamente 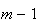 elementos:
elementos: 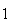 ,
,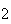 ,
,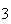 ,...,
,...,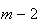 ,
e
,
e 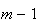 ).
Logo, a diagonal e o lado de
).
Logo, a diagonal e o lado de 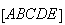 são grandezas incomensuráveis.
são grandezas incomensuráveis.