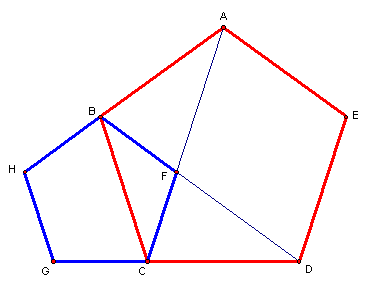
Pentágono regular

Seja 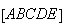 um pentágono regular,
um pentágono regular, 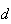 a medida da sua diagonal e
a medida da sua diagonal e 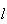 a medida do seu lado. Supondo que
a medida do seu lado. Supondo que 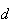 e
e 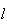 são comensuráveis, temos
são comensuráveis, temos 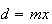 e
e 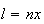 ,
onde
,
onde 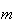 e
e 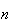 são inteiros positivos e
são inteiros positivos e 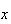 é uma medida comum à diagonal e ao lado do pentágono.
é uma medida comum à diagonal e ao lado do pentágono.
Construindo
a circunferência que circunscreve o pentágono, notemos que os pontos
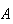 ,
,
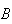 ,
,
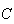 ,
,
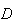 e
e 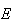 dividem esta em arcos de igual amplitude, dada por
dividem esta em arcos de igual amplitude, dada por 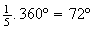 .
Seja
.
Seja 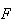 o ponto de intersecção da diagonal
o ponto de intersecção da diagonal ![$\left[ AC\right] $](graphics/pentagono__18.gif) com a diagonal
com a diagonal ![$\left[ BD\right] $](graphics/pentagono__19.gif) .
Como
.
Como 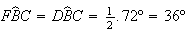 e
e 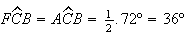 (ângulos inscritos numa circunferência têm como amplitude metade
do valor do respectivo arco), temos que
(ângulos inscritos numa circunferência têm como amplitude metade
do valor do respectivo arco), temos que ![$\left[ FBC\right] $](graphics/pentagono__22.gif) é isósceles, com
é isósceles, com 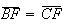 .
Como
.
Como 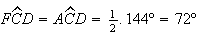 e
e 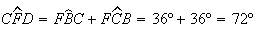 ,
vem que
,
vem que ![$\left[ FCD\right] $](graphics/pentagono__26.gif) também é isósceles, com
também é isósceles, com 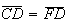 .
Além disso,
.
Além disso, 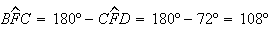 ,
sendo este o valor da amplitude do ângulo interno de um pentágono
regular. Podemos então construir um novo pentágono regular
,
sendo este o valor da amplitude do ângulo interno de um pentágono
regular. Podemos então construir um novo pentágono regular 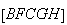 ,
que passa pelos pontos
,
que passa pelos pontos 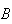 ,
,
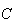 e
e 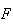 .
Designando por
.
Designando por 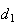 a medida da sua diagonal e
a medida da sua diagonal e 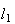 a medida do seu lado, temos:
a medida do seu lado, temos:
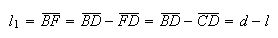
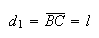
Como 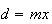 e
e 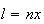 ,
temos:
,
temos:
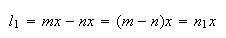
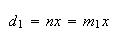
onde 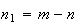 e
e 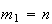 são dois números inteiros positivos, com
são dois números inteiros positivos, com 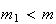 .
De facto, o ângulo de maior amplitude do triângulo
.
De facto, o ângulo de maior amplitude do triângulo ![$\left[ BCD\right] $](graphics/pentagono__44.gif) é o ângulo
é o ângulo 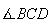 ,
logo a este ângulo opõem-se o lado de maior comprimento e, portanto,
,
logo a este ângulo opõem-se o lado de maior comprimento e, portanto,
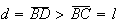 ,
ou seja,
,
ou seja, 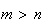 .
.
Procedendo
da mesma forma com o pentágono 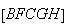 ,
vamos obter um novo pentágono regular cuja diagonal é
,
vamos obter um novo pentágono regular cuja diagonal é 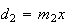 e cujo lado é
e cujo lado é 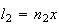 ,
sendo que
,
sendo que 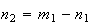 e
e 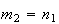 são dois números inteiros positivos, com
são dois números inteiros positivos, com 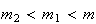 .
.
Uma vez que podemos continuar indefinidamente a construir novos pentágonos regulares, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
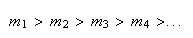
tal que
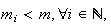 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que 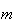 (de facto, existem exactamente
(de facto, existem exactamente 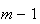 elementos:
elementos: 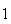 ,
,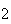 ,
,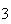 ,...,
,...,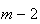 ,
e
,
e 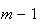 ).
Logo, a diagonal e o lado de
).
Logo, a diagonal e o lado de 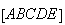 são grandezas incomensuráveis.
são grandezas incomensuráveis.