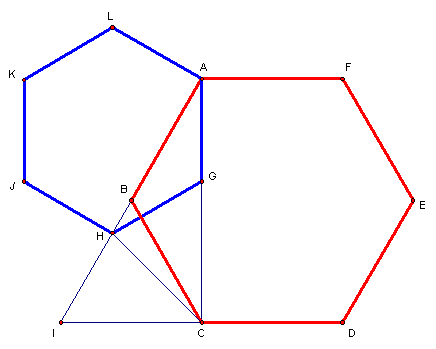
Hexágono regular

Seja 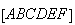 um hexágono regular,
um hexágono regular, 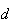 a medida da sua diagonal mais curta e
a medida da sua diagonal mais curta e 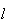 a medida do seu lado. Supondo que
a medida do seu lado. Supondo que 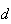 e
e 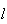 são comensuráveis, temos
são comensuráveis, temos 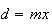 e
e 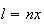 ,
onde
,
onde 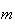 e
e 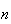 são inteiros positivos e
são inteiros positivos e 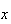 é uma medida comum à diagonal mais curta e ao lado do hexágono.
é uma medida comum à diagonal mais curta e ao lado do hexágono.
Seja 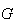 o ponto na diagonal
o ponto na diagonal ![$\left[ AC\right] $](graphics/hexagono__12.gif) tal que
tal que 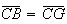 ,
,
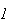 o ponto de intersecção da recta
o ponto de intersecção da recta 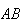 com a recta
com a recta 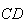 e
e 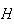 o ponto no segmento de recta
o ponto no segmento de recta ![$\left[ AI\right] $](graphics/hexagono__18.gif) tal que
tal que 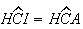 .
Notemos, em primeiro lugar, que o valor da amplitude do ângulo interno
de um hexágono regular é de
.
Notemos, em primeiro lugar, que o valor da amplitude do ângulo interno
de um hexágono regular é de 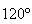 .
Então, como
.
Então, como 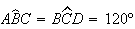 ,
vem
,
vem 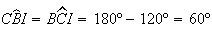 ,
pelo que
,
pelo que ![$\left[ BCI\right] $](graphics/hexagono__23.gif) é um triângulo equilátero. Relativamente aos triângulos
é um triângulo equilátero. Relativamente aos triângulos
![$\left[ CHI\right] $](graphics/hexagono__24.gif) e
e ![$\left[ CHG\right] $](graphics/hexagono__25.gif) ,
temos que
,
temos que 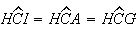 ,
,
 e
e ![$\left[ CH\right] $](graphics/hexagono__28.gif) é um lado comum, logo eles são congruentes, com
é um lado comum, logo eles são congruentes, com 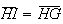 e
e 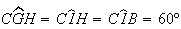 .
Logo,
.
Logo, 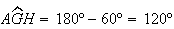 ,
,
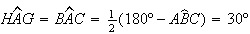 (note-se que
(note-se que ![$\left[ ABC\right] $](graphics/hexagono__33.gif) é isósceles, dado que
é isósceles, dado que 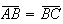 )
e
)
e 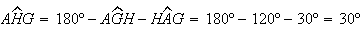 ,
pelo que
,
pelo que ![$\left[ AGH\right] $](graphics/hexagono__36.gif) é isósceles, com
é isósceles, com 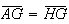 .
Podemos então construir um novo hexágono
.
Podemos então construir um novo hexágono 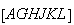 ,
que passa pelos pontos
,
que passa pelos pontos 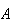 ,
,
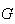 e
e 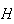 .
Designando por
.
Designando por 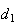 a medida da sua diagonal e
a medida da sua diagonal e 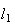 a medida do seu lado, temos:
a medida do seu lado, temos:
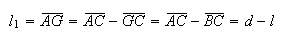
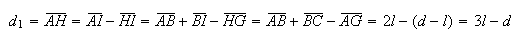
Como 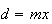 e
e 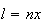 ,
temos:
,
temos:
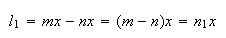
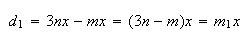
onde 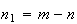 e
e 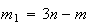 são dois números inteiros positivos, com
são dois números inteiros positivos, com 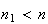 .
De facto,
.
De facto, 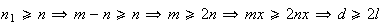 ,
o que é absurdo, uma vez que, em qualquer triângulo, cada lado tem
um comprimento menor do que a soma do comprimento dos outros dois lados; considerando,
por exemplo, o triângulo
,
o que é absurdo, uma vez que, em qualquer triângulo, cada lado tem
um comprimento menor do que a soma do comprimento dos outros dois lados; considerando,
por exemplo, o triângulo ![$\left[ ABC\right] $](graphics/hexagono__54.gif) ,
vem
,
vem 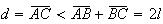 .
.
Procedendo
da mesma forma com o hexágono 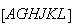 ,
vamos obter um novo hexágono regular cuja diagonal é
,
vamos obter um novo hexágono regular cuja diagonal é 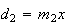 e cujo lado é
e cujo lado é 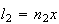 ,
sendo que
,
sendo que 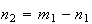 e
e 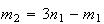 são dois números inteiros positivos, com
são dois números inteiros positivos, com 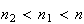 .
.
Uma vez que podemos continuar indefinidamente a construir novos hexágonos regulares, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
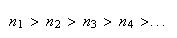
tal que
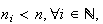 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que 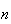 (de facto, existem exactamente
(de facto, existem exactamente 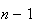 elementos:
elementos: 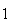 ,
,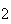 ,
,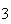 ,...,
,...,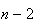 ,
e
,
e 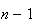 ).
Logo, a diagonal mais curta e o lado de
).
Logo, a diagonal mais curta e o lado de 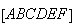 são grandezas incomensuráveis.
são grandezas incomensuráveis.