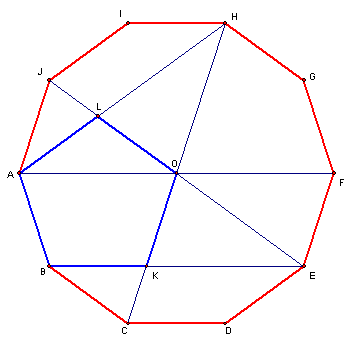
Decágono regular

Seja 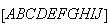 um decágono regular de centro em
um decágono regular de centro em 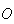 cujas medidas do lado e da diagonal mais longa são
cujas medidas do lado e da diagonal mais longa são 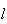 e
e 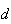 ,
respectivamente. Sejam
,
respectivamente. Sejam
![$\left[ AF\right] $](graphics/decagono4__5.gif) ,
,
![$\left[ CH\right] $](graphics/decagono4__6.gif) e
e ![$\left[ EJ\right] $](graphics/decagono4__7.gif) três diagonais que passam pelo centro do decágono e
três diagonais que passam pelo centro do decágono e ![$\left[ AH\right] $](graphics/decagono4__8.gif) e
e ![$\left[ BE\right] $](graphics/decagono4__9.gif) duas das segundas diagonais mais curtas. Consideremos os pontos
duas das segundas diagonais mais curtas. Consideremos os pontos 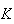 e
e 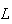 ,
resultantes da intersecção entre as diagonais
,
resultantes da intersecção entre as diagonais ![$\left[ AH\right] $](graphics/decagono4__12.gif) e
e ![$\left[ BE\right] $](graphics/decagono4__13.gif) com as diagonais
com as diagonais ![$\left[ EJ\right] $](graphics/decagono4__14.gif) e
e ![$\left[ CH\right] $](graphics/decagono4__15.gif) ,
respectivamente. Temos que
,
respectivamente. Temos que 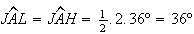 ,
,
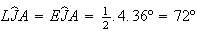 e
e 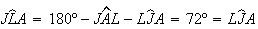 ,
logo
,
logo ![$\left[ AJL\right] $](graphics/decagono4__19.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 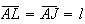 .
Analogamente,
.
Analogamente, ![$\left[ BCK\right] $](graphics/decagono4__21.gif) também é isósceles, com
também é isósceles, com 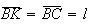 .
Além disso, como estes triângulos são congruentes, temos
.
Além disso, como estes triângulos são congruentes, temos 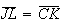 .
O triângulo
.
O triângulo ![$\left[ LAO\right] $](graphics/decagono4__24.gif) também é isósceles, uma vez que
também é isósceles, uma vez que 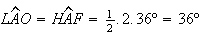 e
e 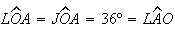 ,
logo
,
logo 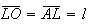 e
e 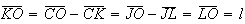 .
Portanto,
.
Portanto, 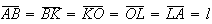 .
Por outro lado, temos que
.
Por outro lado, temos que 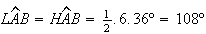 ,
,
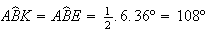 ,
,
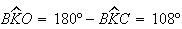 ,
,
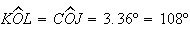 e
e 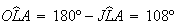 .
Então, o polígono
.
Então, o polígono 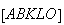 tem os lados todos iguais e os ângulos internos todos iguais, pelo que
é um pentágono regular de lado
tem os lados todos iguais e os ângulos internos todos iguais, pelo que
é um pentágono regular de lado 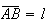 e cuja diagonal é
e cuja diagonal é 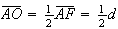 .
Se a diagonal mais longa de
.
Se a diagonal mais longa de 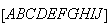 e o seu lado fossem comensuráveis, ou seja, se a razão
e o seu lado fossem comensuráveis, ou seja, se a razão 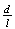 fosse um número racional, então a razão
fosse um número racional, então a razão 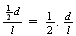 também seria racional e a diagonal de
também seria racional e a diagonal de 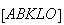 seria comensurável com o seu lado, o que já vimos que não acontece.
Portanto, a diagonal mais longa e o lado do decágono
seria comensurável com o seu lado, o que já vimos que não acontece.
Portanto, a diagonal mais longa e o lado do decágono 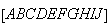 são grandezas incomensuráveis.
são grandezas incomensuráveis.
Nota:
de facto, demonstra-se que a razão entre a diagonal mais longa e o lado
de um polígono regular de 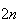 lados, com
lados, com 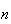 um número ímpar maior do que
um número ímpar maior do que 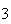 ,
é sempre o dobro da razão entre a diagonal mais longa e o lado de
um polígono regular de
,
é sempre o dobro da razão entre a diagonal mais longa e o lado de
um polígono regular de 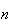 lados. O caso analisado acima corresponde a tomar
lados. O caso analisado acima corresponde a tomar 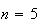 .
Para visualizar o caso seguinte, consulte este
applet.
.
Para visualizar o caso seguinte, consulte este
applet.