(translação) e observe o friso:1. Clique
no botão
(translação) e observe o friso:
a) Encontre
uma translação que deixe o friso invariante (= leve o friso sobre
ele mesmo), executando as instruções indicadas
na página ajuda
(para aceder a esta página clique em 
).
b) Num friso, existem duas translações de comprimento mínimo (não nulo) que o fixam. Verifique se a translação que encontrou em a) é uma translação de comprimento mínimo que fixa o friso em causa e, se não for, procure-a.
c) Existem outras translações diferentes da que indicou que fixam o friso? Em caso afirmativo, qual é a relação (a nível de direcção e de comprimento) entre essas translações e a translação que encontrou na alínea b)?
2. Clique
no botão 
(rotação)
e observe o friso:
a) Encontre
um centro de rotação e um
ângulo diferente de "360º" (ou seus múltiplos) de
forma a obter uma rotação que fixa o friso, executando
as instruções indicadas na página ajuda
(para aceder a esta página clique em ).
b) É possível mudar o ângulo que considerou na alínea a) e obter uma outra rotação (com um ângulo associado maior que 0º e menor que 360º) que fixa o friso? Porquê?
c) É possível mudar a posição do "centro de rotação" por forma a obter outra rotação que também fixa o friso? Em caso afirmativo, quantas são as rotações que fixam o friso (nota: não se esqueça que um friso é ilimitado)?
3. Clique
no botão 
(reflexão
1) e
observe o friso:
a) Mova a recta (e, se quiser, rode-a) por forma a encontrar uma reflexão que fixe o friso em causa.
b) Quantas são as reflexões que fixam o friso?
c) Qual é a a direcção das rectas associadas a estas reflexões?
d) Na imagem abaixo está representado o vector v - vector associado a uma translação de comprimento mínimo que fixa o friso. Encontre, agora, dois eixos de simetria consecutivos do friso (isto é, não existe um eixo de simetria compreendido entre eles). Qual a relação entre a distância destas duas rectas e o comprimento de v?
4.
Clique no botão 
(reflexão 2) e observe o friso:
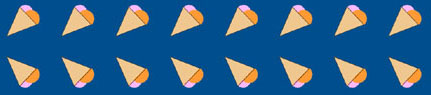
a) Mova a recta (e, se quiser, rode-a) por forma a encontrar uma reflexão que fixe o friso em causa.
b) Quantas são as reflexões que fixam o friso?
c) Qual é a a direcção das rectas associadas a estas reflexões?
5. Considere um friso qualquer e suponha que é horizontal a direcção das translações que fixam o friso, por exemplo
É possível haver uma reflexão numa recta não horizontal e não vertical que fixe esse friso? Em caso afirmativo diga qual é a recta. Em caso negativo explique porquê.
6.
Clique no botão 
-
"Simetria dos passos" (esta simetria é normalmente designada
por reflexão deslizante):
a) Movendo os pontos a preto, encontre o vector associado a uma das translações de comprimento mínimo que fixa o friso - o vector v.
b) Mova a recta e tente encontrar uma reflexão que fixe o friso. O que conclui?
c) Mova agora a recta para a posição indicada na figura:
É fácil perceber que a reflexão nesta recta não fixa o friso. Mas, se reflectir o friso nessa mesma recta
e, de seguida, efectuar uma translatação segundo o vector v1 assinalado na figura abaixo.
obtém uma isometria que fixa o friso. Essa isometria é designada "reflexão deslizante"*. Veja a animação abaixo:
c1) Qual é a relação entre v1 e v (=vector encontrado na alínea a))?
c2) Repare que se reflectir o friso na recta e depois efectuar uma translação segundo o vector v2, obtém ainda uma reflexão deslizante que fixa o friso. O mesmo se passa se utilizar o vector v3. O que conclui acerca do número de reflexões deslizantes que fixam o friso?
* Uma reflexão deslizante é a composta de uma reflexão numa recta com uma translação na direcção dessa recta.
