I. Interpretar o problema
A primeira questão colocada por este problema é: fixados dois pontos na caixa, como determinar a trajectória que minimiza o comprimento a percorrer entre estes dois pontos?

No estudo deste problema, surge a noção de uma nova métrica, diferente da métrica usual no espaço R3, pois consideramos apenas trajectórias sobre a superfície da caixa e nunca trajectórias que atravessem o seu interior.
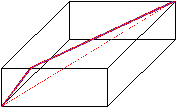
A procura de soluções para a determinação da distância entre dois pontos A e B, segundo esta nova métrica, passa pela planificação da caixa:
| Ao considerar algumas das trajectórias que passem por determinadas faces da caixa, o menor comprimento é o que é dado pelo segmento de recta que une os dois pontos numa planificação adequada. | 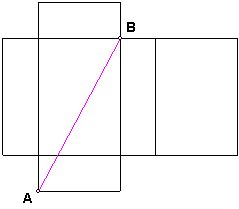 |
| Mas existem várias possibilidades de unir os dois pontos através de um segmento, pelo que, para determinar qual a distância entre estes pontos, devemos considerar diferentes planificações da caixa e comparar os seus comprimentos. | 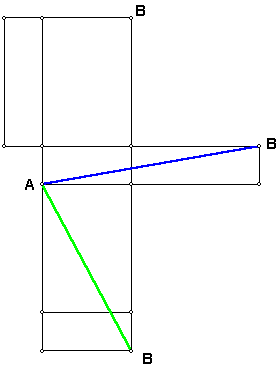 |
Na definição desta nova métrica, a distância entre quaisquer dois pontos da caixa é dada pelo menor comprimento de todas as trajectórias que unam os pontos.
Desta primeira análise do problema, surgem várias questões:
r Como podemos determinar a distância entre quaisquer dois pontos da caixa ?
r Será possível limitar o número de trajectórias que devemos considerar para determinar o menor comprimento a percorrer?
r Qual será, para um ponto fixo na caixa, o ponto da caixa que se encontra a maior distância deste, considerando esta nova métrica ?
r E se variarmos as dimensões da caixa ? De que modo é que esta variação altera as respostas às perguntas anteriores ?
..