



 |
O primeiro objecto da Exposição que encontra
no Pavilhão do Conhecimento, ainda no exterior, junto aos repuxos
de água, está representado nas fotos juntas.
|
 |
 O gif animado
junto,
reproduz, em versão acelerada (ver o movimento das pessoas ao fundo),
aquilo que o visitante pode observar no local.
O gif animado
junto,
reproduz, em versão acelerada (ver o movimento das pessoas ao fundo),
aquilo que o visitante pode observar no local.
O que ilustra este módulo?
Imaginemos uma recta (ou um segmento de recta) a rodar em torno de outra recta (o eixo de rotação); se a recta móvel deixasse rasto, qual seria esse rasto? (Os matemáticos perguntariam: qual seria a superficie gerada por essa recta móvel?)
Há três casos a distinguir:
Caso 1: 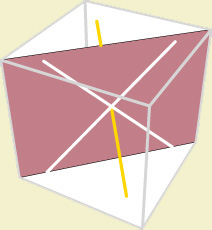 Intersectam
em duas rectas igualmente inclinadas; se quiser ter uma visão tridimensional
do cone
Intersectam
em duas rectas igualmente inclinadas; se quiser ter uma visão tridimensional
do cone  e de algumas rectas
e de algumas rectas  ,
que dão já uma ideia desse cone, clique numa destas duas
figuras e use o rato na nova janela.
,
que dão já uma ideia desse cone, clique numa destas duas
figuras e use o rato na nova janela.
Caso 2: 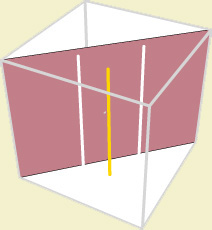 Intersectam
em duas rectas paralelas ao eixo de rotação, a igual distância
deste; se quiser ter uma visão tridimensional do cilindro
Intersectam
em duas rectas paralelas ao eixo de rotação, a igual distância
deste; se quiser ter uma visão tridimensional do cilindro  e de algumas rectas
e de algumas rectas  ,
que dão já uma ideia desse cilindro, clique numa destas duas
figuras e use o rato na nova janela.
,
que dão já uma ideia desse cilindro, clique numa destas duas
figuras e use o rato na nova janela.
Caso 3: 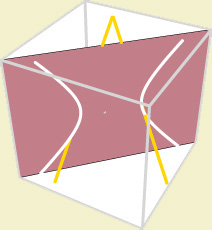 Intersectam
numa hipérbole; se quiser ter uma visão tridimensional do
hiperboloide
Intersectam
numa hipérbole; se quiser ter uma visão tridimensional do
hiperboloide 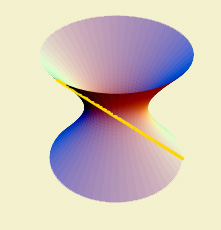 e de algumas rectas
e de algumas rectas  ,
que dão já uma ideia desse hiperboloide, clique numa destas
duas figuras e use o rato na nova janela.
,
que dão já uma ideia desse hiperboloide, clique numa destas
duas figuras e use o rato na nova janela.
Questão interessante:
No caso 3, a recta móvel vai ocupando uma infinidade de posições. Claro que qualquer dessas rectas intermédias, posta a rodar, deixa o mesmo rasto (isto é, gera a mesma superfície). É natural perguntar se, quando tomarmos uma recta diferente dessas todas, obtemos necessariamente uma superfície diferente. A resposta é negativa: há outra recta que, rodando em torno do mesmo eixo, deixa exactamente o mesmo rasto. Essa recta móvel vai também ocupando uma infinidade de posições e claro que também qualquer dessas rectas intermédias, posta a rodar, deixa o mesmo rasto (isto é, gera a mesma superfície). Mas não há mais rectas nessas condições, além destas duas infinidades de rectas: qualquer recta diferente destas deixa um rasto diferente (isto é, gera um hiperboloide diferente) ...
No interior, irá encontrar outro módulo - o hiperboloide de fios -, relacionado com este.
|
|
|
|