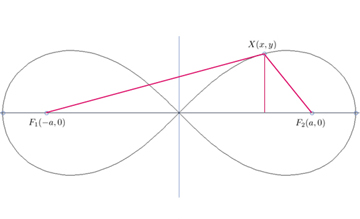
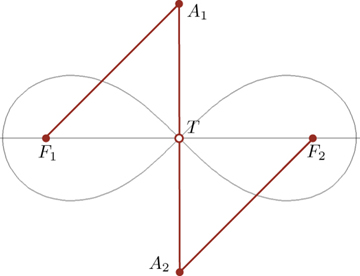
Em 1694, Jacob Bernoulli publicou um artigo na famosa Acta Eruditorum , no qual descrevia uma curva plana, que designou por lemniscus. Actualmente, essa curva é conhecida pela designação de lemniscata de Bernoulli. Catorze anos antes, no ano de 1680, Cassini já tinha descrito, de modo genérico, uma família de curvas planas, conhecidas actualmente por ovais de Cassini. Mas, muito embora a lemniscata seja um caso particular de uma oval de Cassin, na época de Bernoulli não havia ainda consciência desse facto. Só mais tarde quando as propriedades daquelas curvas foram sendo conhecidas e as suas caracterizações mais diversificadas, um tal facto se tornou claro. Grandes matemáticos como Gauss e Euler também se ocuparam do estudo da lemniscata. De resto, no caso de Gauss, foram precisamente as suas investigações acerca do comprimento de arco da lemniscata, que o conduziram ao desenvolvimento da teoria das funções elípticas. Quem, contudo, primeiro forneceu uma descrição analítica da lemniscata foi Giovanni Fagnano, em 1750.

Descrição geométrica: em termos geométricos, a lemniscata possui uma caracterização muito parecida com a da elipse: dados dois pontos F₁ e F2, que se designam "focos", os pontos, X, da lemniscata são os pontos do plano que satisfazem a condição de o produto das distâcias de X a F₁ e a F2 ser constante (no caso da elipse é a soma dessas distâncias que é constante).

Na figura 1 encontra-se representada a lemniscata correspondente ao caso em que o produto das distâncias é a². Neste caso a distância entre os focos (F₁ e F2) é 2a.

De entre os vários engenhos mecânicos que permitem desenhar uma lemniscata, destaca-se, pela sua simplicidade, aquele que se descreve na figura 2.

O mecanismo consiste basicamente de um antiparalelogramo articulado. Os pontos F₁ e F2 estão fixos e correpondem aos focos da lemniscata. Os segmentos [F₁A₁], [A₁A2] e [A2F2], podem imaginar-se de um material rígido. As uniões em A₁ e A2, são articuladas. Considerando o mecanismo que acabámos de descrever, se fizermos deslocar o segmento [A₁A2] para que A₁ e A2 descrevam circunferências de modo a que A₁ e A2 nunca se encontrem no mesmo semiplano deteminado pela recta F₁F2. Então, o ponto médio do segmento [A₁A2], denotado por T, traça, no seu deslocamento, uma lemniscata.