|
Genética*
|
|
Nesta secção examinaremos a transmissão hereditária de traços, que suporemos ser regidos por dois genes, digamos A e a, e cuja herança segue leis de hereditariedade autossómica. Isto significa que:
O efeito das condições (a) e (b) está descrito na tabela seguinte que revela a probabilidade de ocorrência dos possíveis genótipos nos descendentes:
Por exemplo,
se os pais têm genótipos aa e Aa, o descendente recebe com
igual probabilidade ( Suponhamos agora que um horticultor tem uma plantação de roseiras, planta que tem floração de pelo menos três cores: vermelha (correspondente ao genótipo AA), rosa (de genótipo Aa) e branca (de genótipo aa).
Admitamos que o horticultor quer empreender um programa de hibridação (regra 1) em que cada planta é fertilizada por uma de genótipo AA. O que esperar das flores em gerações seguintes? Utilize este programa para verificar se a sua conjectura é verdadeira. |
|||||||||||||||||||||||||||||||||||

|
Note-se
que, como são proporções, para todo o n, temos
Por
exemplo, a primeira das equações deduz-se do facto que, neste esquema de fertilização
só com plantas de genótipo AA, todos os descendentes de uma planta
de genótipo AA (e na plantação há uma fracção vn-1
delas) têm este genótipo; além disso, em termos probabilísticos, metade dos
descendentes das plantas com genótipo Aa tem chance de nascer com genótipo
AA, igualmente contabilizado em vn.
e pode-se concluir [ver aqui] que
A vantagem desta escrita é que temos as proporções vn, rn e bn formuladas em termos dos valores fixos iniciais. O que nos permite concluir que
o que significa que, a longo prazo, o horticultor obterá sobretudo plantas de flores vermelhas.
Repare que esta conclusão é independente de quantas flores há de cada cor à partida (supondo que há pelo menos uma rosa vermelha). Repare no seguinte quadro que dá a evolução ao longo das várias gerações, partindo de percentagens diferentes no início.
Observe-se
que, não surpreendentemente (Porquê?), o limite de O que esperaria que acontecesse em gerações futuras se o horticultor quisesse experimentar um programa de hibridação em que cada planta é fertilizada por uma com o seu genótipo (regra 2)? Pode confirmar essa conjectura? Depois de o fazer, consulte um quadro semelhante ao anterior aqui. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Estes conteúdos utilizam
|
*Realização no âmbito do projecto "Conteúdos virtuais de Topologia e Sistemas dinâmicos" do Programa Apoio C&T, apoiado pelo
|

 ,
então x(n+1) = Mx(n), onde
M é a matriz formada pelas três colunas da tabela acima que aqui importam:
,
então x(n+1) = Mx(n), onde
M é a matriz formada pelas três colunas da tabela acima que aqui importam:
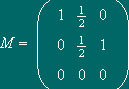
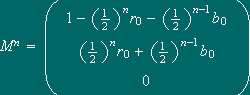





























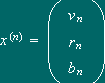 é um vector fixo pela matriz M.
é um vector fixo pela matriz M.