ATRACTOR

Sometimes diagrams may be misleading!

Consider the following summation:

\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...=?\)

This summation is represented by gray region in the following chart (each block corresponds to one summand):

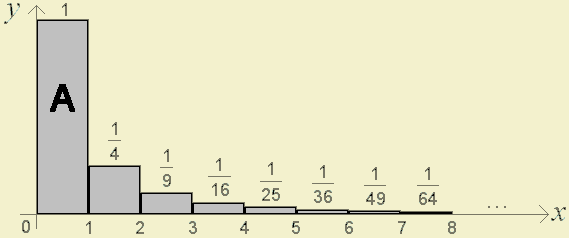
(Observation: The scales in x-axis and y-axis are different.)

Then, comparing each corresponding block, the previous summation is smaller than the coloured area in the following diagram:

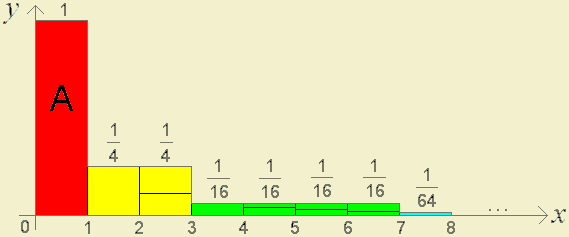
In fact,

\(\begin{array}{ccc} 1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...\\ =\\ 1 & = & 1\\ +\frac{1}{4}+\frac{1}{9} & < & 2\times\frac{1}{4}=\frac{1}{2}\\ +\frac{1}{16}+\frac{1}{25}+\frac{1}{36}+\frac{1}{49} & < & 4\times\frac{1}{16}=\frac{1}{4}\\ +\frac{1}{8^{2}}+\frac{1}{9^{2}}+...+\frac{1}{15^{2}} & < & 8\times\frac{1}{64}=\frac{1}{8}\\ ... & ... & ...\\ +\frac{1}{(2^{n})^{2}}+\frac{1}{(2^{n}+1)^{2}}+...+\frac{1}{(2^{n}+(2^{n}-1))^{2}} & < & 2^{n}\times\frac{1}{(2^{n})^{2}}=\frac{1}{2^{n}}\\ ... & ... & ... \end{array}\)

and, therefore,

\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...<1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^{n}}+...=2\)

So, if we would need one gray paint can to colour the quadrilateral A (with area 1) in the first diagram, we would need two paint cans (with some leftover paint) to colour the entire gray region.

Consider now the summation

\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{n}+...\)

and the corresponding diagram.

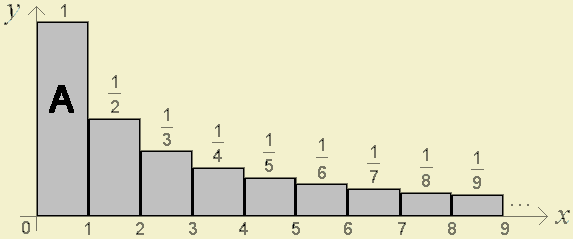
How many paint cans would be needed to paint the gray region? Comparing this picture with the first one, we are led to say that just a little more paint will suffices (maybe three or four cans). Is it really so? We have

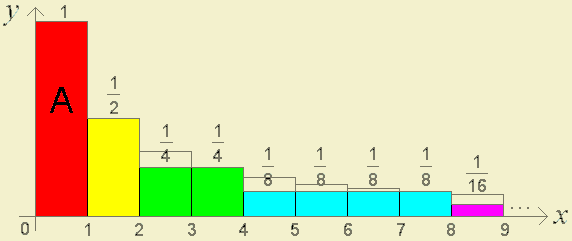
that is,

\(\begin{array}{ccc} 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{n}+...\\ =\\ 1 & = & 1\\ +\frac{1}{2} & = & \frac{1}{2}\\ +\frac{1}{3}+\frac{1}{4} & >& 2\times\frac{1}{4}=\frac{1}{2}\\ +\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8} & > & 4\times\frac{1}{8}=\frac{1}{2}\\ +\frac{1}{9}+\frac{1}{10}+...+\frac{1}{16} & > & 8\times\frac{1}{16}=\frac{1}{2}\\ ... & ... & ...\\ +\frac{1}{(2^{n}+1)}+\frac{1}{(2^{n}+2)}+...+\frac{1}{(2^{n+1})} & > & 2^{n}\times\frac{1}{(2^{n+1})}=\frac{1}{2}\\ ... & ... & ... \end{array}\)

and, therefore,

\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{n}+...>1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+...\)

This means that there is not enough paint in the Universe to colour all the coloured region, which contradicts our conjecture that three or four paint cans would suffice.

Conclusion:

Although the two diagrams are quite similar, the properties of the corresponding summations are pretty different. The mistake this time is not in the lack of rigour in diagrams, but in the fact that they only represent a small (finite) part of the total summation (which has an infinite number of summands) and consequently do not allow us to draw conclusions about the value of the summation. The step from the finite to the infinite in Mathematics may bring many surprises!