Os Números Quadrados

Como seria de suspeitar, um Número Quadrado resulta de se elevar ao quadrado um número inteiro e que, por isso mesmo, representa numa área quadrada. Concordemos que esta é uma definição perfeitamente "quadrada".

Neste caso, a melhor definição é a própria Fórmula Fechada:   Q(n) = n²

Vejamos os primeiros Números Quadrados:

Q(1)= 12 = 1

Q(2)= 22 = 4

Q(3)= 32 = 9

Q(4)= 42 = 16

Procuremos a Relação Recursiva que traduz este processo:

Para passar de um dado quadrado de lados igual a n, ao quadrado seguinte (n+1)2, precisamos de juntar duas filas de comprimento n e mais uma unidade para o canto. Ou seja: Q(n+1) = Q(n) + n + n + 1 Assim chegamos à Fórmula Recursiva: Q(1) = 1 Q(n+1) = Q(n) + (2n + 1)

Recapitulemos todo o processo de construção, desde o quadrado unitário:

Q(1) = 1 = 12 Q(2) = Q(1) + 3 = 1 + 3 = 22 Q(3) = Q(2) + 5 = 1 + 3 + 5 = 32 Q(4) = Q(3) + 7 = 1 + 3 + 5 + 7 = 42 Q(5) = Q(4) + 9 = 1 + 3 + 5 + 7 + 9 = 52 ... Q(n) = Q(n-1) +(2n-1) = 1 + 3 + 5 + ... + (2n-1) = n2

Verificamos assim que a soma dos primeiros n números ímpares é igual a n², o que também já não era novidade na antiga Grécia:

Fórmula Iterativa:   Q(n) = 1 + 3 + 5 + ... + (2n-1)

Podemos demonstrar este resultado de outro modo, utilizando Números Triangulares:

Tomemos a sequência dos n primeiros números ímpares,   1 + 3 + 5 + 7 + 9 + ... + (2n-1) e retiremos uma unidade a cada um,   0 + 2 + 4 + 6 + 8 + ... + (2n-2) guardando os n elementos que retirámos (coluna a vermelho). Como todos os termos da sequência obtida são números pares,   2 ( 1 + 2 + 3 + 4 + ... + (n-1)) o que representa dois triângulos de ordem (n-1). Combinando os dois triângulos T(n-1) com os n elementos guardados obtemos, por fim, o quadrado Q(n):   2 T(n-1) + n = (n-1)*n + n = n2 - n + n = n2.

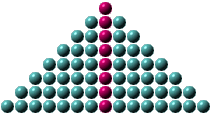
1+3+5+7+9+11+13+15 2 T(7) + 8 = 82

Teorema Q1 (Nicómacus, sec. I):   T(n) + T(n+1) = Q(n+1)

Este é o nosso conhecido Teorema T2.

Teorema Q2 (Plutarco, sec I):
Se T fôr um Número Triangular, então 8 T + 1 é um Número Quadrado:

A demonstração consiste apenas em combinar 8 triângulos iguais, de forma conveniente:

8  *   =   4  *	Tomemos os 8 triângulos T(n) dados. Pelo Teorema T1 podemos juntá-los aos pares, obtendo 4 rectângulos, 8 T(n) = 4 (2 T(n)) = 4 (n (n+1)).
4  *	Mas,   4 (n (n+1)) = 4 n2 + 4 n o que representa 4 quadrados mais 4 colunas.
	Combinando 4 quadrados com 4 colunas e mais uma unidade, temos então: 4 n2 + 4 n + 1 = (2n + 1)2 isto é,   8 T(n) + 1 = Q(2n + 1) .

Acontece, ainda, que   8 T(n) + 1 = Q(2n + 1) = T(n-1) + 6 T(n) + T(n+1)

mas não lhe vamos roubar o prazer de descobrir como...

As Origens de um Jogo:

Parece ter sido Arquimedes quem inventou uma divisão do quadrado em 14 partes, que esteve na origem do célebre jogo chinês Tangram, em que se procura construir diversas figuras, a partir de 7 partes de um quadrado.

por Rosália Rodrigues e Emília Miranda

De "As Formas e os Números"