Os Números Pentagonais
A noção de Número Pentagonal é um pouco mais subtil, senão vejamos:
|
A unidade é o primeiro Número Pentagonal, assim como foi o primeiro Número
Triangular e o primeiro Número Quadrado, assim como vai ser o primeiro
de "quase" tudo o que aqui se irá passar. |

P(1)=1
|
O segundo Número Pentagonal é naturalmente o menor número de bolas
com que podemos formar um pentágono, ou seja, P(2) = 5.
Para construir P(2) a partir de P(1) juntamos 4 bolas.
|

P(2)=5
|
A partir do canto inferior esquerdo, vamos acrescentando
bolas, de modo a formar um novo pentágono de lados iguais a três.
O total obtido é o terceiro Número Pentagonal, P(3) = 12.
Verificamos que P(3) = P(2) + 7 e que, desta vez, não vai ser possível
preencher os espaços interiores com uma distribuição regular de bolas. |

P(3)=12
|
Procuremos a Relação Recorrente geral:
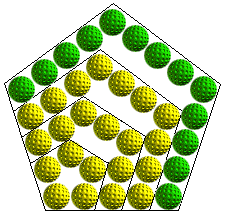
P(5) = P(4)+(3*5-2) = 22+13 = 35
|
Para passar do Número Pentagonal de ordem n ao seguinte, P(n+1),
precisamos de juntar três lados de comprimento igual a n+1, não esquecendo
de descontar as duas sobreposições nos cantos, isto é:
P(n+1) = P(n) + 3 (n+1) - 2 = P(n) + 3n + 1.
Assim chegamos à Fórmula Recursiva:
P(1) = 1
P(n+1) = P(n) + (3n + 1).
|
Do mesmo modo, para construir P(n) juntamos 3n-2 bolas ao anterior.
Recapitulando:
P(1) = 1 = 1
P(2) = P(1) + 4 = 1 + 4 = 5
P(3) = P(2) + 7 = 1 + 4 + 7 = 12
P(4) = P(3) + 10 = 1 + 4 + 7 + 10 = 22
P(5) = P(4) + 13 = 1 + 4 + 7 + 10 + 13 = 35
...
P(n) = P(n-1) + (3n-2).
E já temos a Fórmula Iterativa:
P(n) = 1 + 4 + 7 + 10 + 13 + ... + (3n - 2).
|
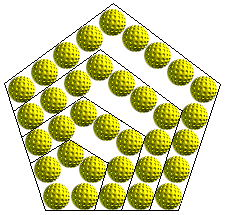 |
Embora não pareça, pelo menos à primeira vista, os Números Pentagonais
são "quase triangularizáveis".
Teorema P1: P(n) = 3 T(n-1) + n
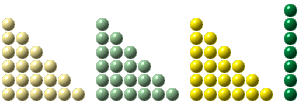 |
Tomemos os três triângulos T(n-1) dados, na sua forma iterativa:
3 (1 + 2 + 3 + 4 + ... (n-1)) =
3 + 6 + 9 + 12 + ... + (3n-3).
|
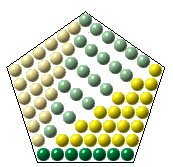 |
Juntando a estas (n-1) parcelas, uma a uma, os n elementos também dados:
1 + 4 + 7 + 10 + 13 + ... + (3n-2)
obtemos precisamente a forma iterativa de P(n).
|
Com este resultado, escrevendo os Números Triangulares na sua Fórmula
Fechada,
P(n) = 3 T(n-1) + n = 3 (n-1) n / 2 + n
é fácil obter a Fórmula Fechada dos Números Pentagonais:
P(n) = (n/2) (3n - 1).
Mais surpreendente, é que alguns Números Triangulares são "pentagonizáveis".
Teorema P2: 3 P(n) = T(3n-1)
|
Em termos puramente algébricos, este facto é consequência imediata da
fórmula anterior:
3 P(n) = 3 (n/2) (3n-1) = (3n) (3n-1) / 2 = T(3n-1).
Em termos geométricos, basta invocar o Teorema P1:
3 P(n) = 3 (3 T(n-1) + n) = 9 T(n-1) + 3n
|

9 T(4) + 3 * 5 = T(14) |
O resultado seguinte sugere uma alternativa para o desenho do pentágono.
Teorema P3: P(n) = Q(n) + T(n-1)
|
Invocando os Teoremas T1, Q1 e P1,
P(n) = 3 T(n-1) + n = 2 T(n-1) + n + T(n-1) = Q(n) + T(n-1).
|

P(5) = Q(5) + T(4) |