Os Números Hexagonais

À semelhança dos casos anteriores, o primeiro Número Hexagonal é a unidade e o segundo é o menor número de bolas com as quais podemos desenhar um hexágono regular.

H(1) = 1

H(2) = 6

H(3) = 15

Claro que a unidade não precisava de ser tão grande, nem sequer precisava de tentar imitar madeira, mas concordemos que a bola é bonita.

Procuremos a Relação Recorrente geral:

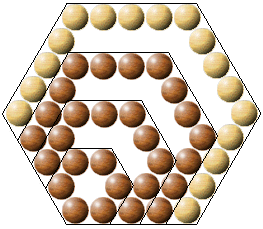
H(5) = H(4)+(4*5-3) = 28+17 = 45

Para passar do Número Hexagonal de ordem n ao seguinte, H(n+1), precisamos de juntar quatro lados de comprimento igual a n+1, não esquecendo de descontar as três sobreposições nos cantos, isto é: H(n+1) = H(n) + 4 (n+1) - 3 = H(n) + 4n + 1. Assim chegamos à Fórmula Recursiva: H(1) = 1 H(n+1) = H(n) + (4n + 1).

Do mesmo modo, para construir H(n) juntamos 4n-3 bolas ao anterior.

Recapitulando: H(1) = 1 = 1 H(2) = H(1) + 5 = 1 + 5 = 6 H(3) = H(2) + 9 = 1 + 5 + 9 = 15 H(4) = H(3) + 13 = 1 + 5 + 9 + 13 = 28 H(5) = H(4) + 17 = 1 + 5 + 9 + 13 + 17 = 45 ... H(n) = H(n-1) + (4n-3) E já temos a Fórmula Iterativa: H(n) = 1 + 5 + 9 + 13 + 17 + ... + (4n - 3)

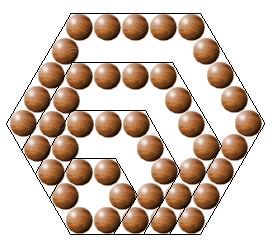Continuando a explorar a evidente analogia com os Números Pentagonais, podemos também deduzir que os os Números Hexagonais são "quase triangularizáveis".

Teorema H1:   H(n) = 4 T(n-1) + n

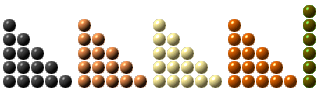	Tomemos os quatro triângulos T(n-1) dados, na sua forma iterativa:   4 (1 + 2 + 3 + 4 + ... (n-1)) =   4 + 8 + 12 + 16 + ... + (4n-4).
	Juntando a estas (n-1) parcelas, uma a uma, os n elementos também dados: 1 + 5 + 9 + 13 + 17 + ... + (4n-3) obtemos precisamente a forma iterativa de H(n). (Notamos também que a presença dos espaços está, neste caso, a tornar-se mais incómoda, pelo menos em termos gráficos. Começamos, contudo, a suspeitar que existe uma certa regularidade nos próprios espaços.)

Com base no Teorema H1, e escrevendo os Números Triangulares na sua Fórmula Fechada,

  H(n) = 4 T(n-1) + n = 4 (n-1) n / 2 + n

é fácil obter a Fórmula Fechada dos Números Hexagonais:

    H(n) = n (2n - 1).

Para além das analogias com os Números Pentagonais, os Números Hexagonais possuem características muito próprias. Acontece, por exemplo, que todo o Número Hexagonal é efectivamente um Número Triangular.

Teorema H2:   H(n) = T(2n-1)

Analisemos a Fórmula Iterativa de T(2n-1).

 T(2n-1) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... + (2n-2) + (2n-1)

Como as parcelas são em número ímpar podemos, começando na segunda, 
somá-las aos pares,

 T(2n-1) = 1 + (2+3) + (4+5) + (6+7) + (8+9) + ... + (2n-2+2n-1)
         = 1 + 5 + 9 + 13 + 17 + ... + (4n-3)

o que é precisamente a Fórmula Iterativa de H(n).

Com efeito, se compararmos a construção de um Número Hexagonal com a de um Número Triangular, vemos que cada nova camada no hexagonal tem o mesmo número de bolas que duas novas camadas no triangular.

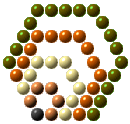
H(5)

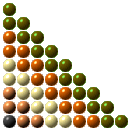
T(9)

Todo o Número Hexagonal é um Número Triangular mas nem todo o Número Triangular é um Número Hexagonal. Basta notar que só são hexagonais os triangulares que resultam de se juntar pares de camadas à unidade, isto é, só são hexagonais os números triangulares de ordem ímpar.

 

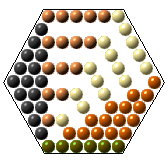
Teorema H3:   H(n) = Q(n) + 2 T(n-1)

Sendo H(n) = T(2n-1), retomemos a Fórmula Iterativa de T(2n-1),

 T(2n-1) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... + (2n-2) + (2n-1)

e agora separemos as parcelas pares das parcelas ímpares, T(2n-1) = 1 + 3 + 5 + 7 + 9 + ... + (2n-1) + 2 + 4 + 6 + 8 + 10 + ... + (2n-2) = 1 + 3 + 5 + 7 + 9 + ... + (2n-1) + 2 (1 + 2 + 3 + 4 + 5 + ... + (n-1)) = Q(n) + 2 T(n-1)

H(5) = Q(5) + 2 T(4)

 

E assim conseguimos desenhar um Número Hexagonal, com a forma de um hexágono e sem espaços interiores. Perdemos a regularidade do polígono e também o equilíbrio estético da forma inicial, que nos proporcionou a intuição do conceito.

 

Já agora, e para quem preferir formas realmente compactas, recordemos a Fórmula Fechada dos Números Hexagonais: H(n) = n (2n - 1)

H(5) = 5 * 9

por Rosália Rodrigues e Emília Miranda

De "As Formas e os Números"