ATRACTOR

• \(\left\{ 1,2,3,4,5,6\right\} \)

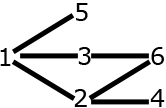
This set doesn't have a maximum for \(\trianglelefteq\), although \(6\) is a maximum for the usual order.

• \(\left\{ 2,3,5,6,10,30\right\} \)

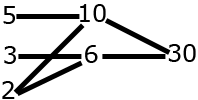
30 is the maximum of this set for \(\trianglelefteq\) and for the usual order.

• \(\left\{ 2,4,6,8,12,16\right\} \)

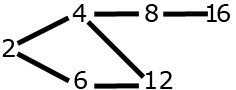
This set doesn't have a maximum for \(\trianglelefteq\) (although \(16\) is a maximum for the usual order).

What we are interested in is the case of the set of divisors of a number or of the set of common divisors of two numbers.

• divisors of \(12\): \(\left\{ 1,2,3,4,6,12\right\} \)

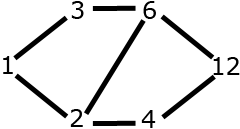
12 is the maximum for \(\trianglelefteq\)

• divisors of \(36\): \(\left\{ 1,2,3,4,6,9,12,18,36\right\} \)

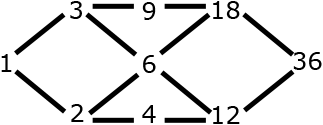
\(36\) is the maximum for \(\trianglelefteq\)

• divisors of \(60\): \(\left\{ 1,2,3,4,5,6,10,12,15,20,30,60\right\} \)

  

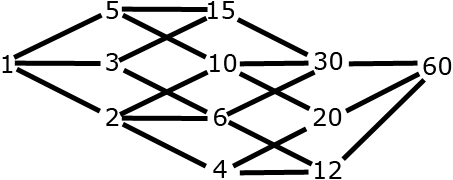
\(60\) is the maximum for \(\trianglelefteq\)

• common divisors of \(12\) and \(18\): \(\left\{1,2,3,6\right\} \)

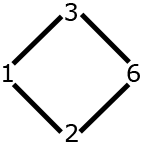
\(6\) is the maximum for \(\trianglelefteq\)

• common divisors of \(50\) and \(30\): \(\left\{1,2,5,10\right\} \)

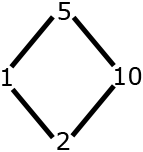
\(10\) is the maximum for \(\trianglelefteq\).