Cylinder - get to know the surface
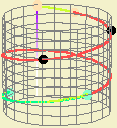
We can think of a cylinder (that is, a cylindrical surface) as a surface which can be obtained by gluing parallel sides of a rectangle without twists. The non-glued sides define each a simple closed curve, as a circunference.
In this way, we identify the points in the rectangle with the points in the cylinder. \[(u,v)\rightarrow(r\cos(u),r\sen(u),v).\] The points of the glued rectangle sides correspond to a segment in the cylinder. This gives us an identification of the parallel sides illustrated by its coloration.
Drawing a circle in the cylinder which intersects the glued segment once, corresponds in the rectangle to draw an arc connecting two points of the identified sides at the same hight.
The longitude and latitude of the points give us the coordenates of its location on the surface. The latitude varies in an closed interval \(I\) in \(\mathbb{R}\) and is measured in hight (in the case of our apps). The longitude is the measure of an angle (in radians) with respect to the position of the point around the surface. Considering the longitude represented in the interval \(\left[0,2\pi\right[\) we cover the whole surface.
However, we can also use different intervals to identify the longitude, for continuous identification of the curve, with the following identification: \[\begin{array}{ccc} J\times I & \rightarrow & \left[0,2\pi\right[\times I\\ (u,v) & \rightarrow & (\mbox{Mod}\left[u,2\pi\right],v) \end{array}\]
This extension is noticed in the apps by a change of scale, such we can better analise the curves that wrap around the cylinder several times.
This lift of the paths in the cylinder to the rectangle can be extended to a planar strip, allowing us to, simultaneously, study all curves in the cylinder, without restriction on the number of times arounf the cylinder. We consider analogously, infinite "copies" of the rectangle, properly aligned; we can then say that each point of this planar strip projects to a point of the cylinder, and that each point of the cylinder lifts to an infinitude of points in the planar strip, each in one of the rectangles.