fig.1	fig.2

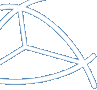
Nota: se clicar na figura 1, obterá esta figura em tamanho maior e tem, por exemplo, a possibilidade de a pôr a "rodar" no espaço (arrastando-a com o rato).

Uma das características da geometria esférica mais distante da geometria euclidiana a que estamos mais habituados, é o facto de que não existe a noção de semelhança: ou seja, não podemos, tal como num plano, desenhar duas figuras que tenham exactamente a mesma forma, mas em que uma seja um pouco maior e a outra um pouco menor. O tamanho condiciona a forma, e vice-versa: não podemos encontrar um triângulo esférico que seja maior do que o observado na figura ao lado, e que tenha os mesmos ângulos. Podemos, naturalmente, partir de uma esfera maior, mas se os ângulos são de 90, 60 e 45 graus, a área do triângulo será, de qualquer forma, 1/48 da área da esfera. A área de um triângulo é, na verdade, proporcional ao seu excesso angular.

Será que também existem triângulos “magros” para além dos triângulos gordos? Ou seja, triângulos cuja soma dos ângulos é inferior a 180 graus? A resposta é afirmativa, e a geometria correspondente é a geometria hiperbólica. A figura 2 (que lembra a estrutura de alguns desenhos de Escher) é uma “irmã” das esferas correspondentes aos caleidoscópios; aqui também se encontram alguns “triângulos” (magros), todos iguais entre si, só que, desta vez, os ângulos são de 90º, 60º e (360/14)º.

E “a beleza” reside no facto de a situação ser totalmente “simétrica” relativamente à que encontramos para a geometria esférica. Também na geometria hiperbólica não existe noção de semelhança; a soma dos ângulos de um triângulo é sempre inferior a um ângulo raso, a forma de um triângulo determina o seu tamanho, e a área de um triângulo é proporcional ao seu defeito angular, isto é, o que falta à soma dos ângulos para ser o ângulo raso.

Mas este é apenas o início de uma longa história….