Plane - fundamental group
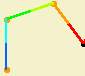
In the plane, any two paths with the same end points are homotopic. One simple way to imagine a homotopy in the plane is to consider the segments between a point in a path and the corresponding point in the other path, as we walk through each path simultaneously. Note that in the plane this is always possible. As the paths are continuous, this family of segments is also continuous, it starts in the start point (of both segments), goes through all segments until it reaches the end point (of both paths).
Formally, given two continuous paths \(f_{1}\) and \(f_{2}\) from \([0,1]\) to the plane, with \(f_{1}(0)=f_{2}(0)\) and \(f_{1}(1)=f_{2}(1)\), a homotopy \(H\) from \([0,1]\times[0,1]\) to the plane (between \(f_{1}\) and \(f_{2}\)) can be defined by: \[H(t,x)=f_{1}(t)+x(f_{2}(t)-f_{1}(t))=\\\;\;\;\;\;\;=(1-x)f_{1}(t)+xf_{2}(t)\]
Note that \(H\) is continuous, \(H(t,0)=f_{1}(t)\), \(H(t,1)=f_{2}(t)\), \(H(0,x)=f_{1}(0)=f_{2}(0)\) and \(H(1,x)=f_{1}(1)=f_{2}(1)\), then the homotopy is well defined. Moreover, with respect to the description above, for each \(t_{0}\) of \([0,1]\), \(H(t_{0},x)=(1-x)f_{1}(t_{0})+xf_{2}(t_{0})\) is the segment connecting \(f_{1}(t_{0})\) to \(f_{2}(t_{0})\) and, in particular, \(H(0,x)=f_{1}(0)=f_{2}(0)\) and \(H(1,x)=f_{1}(1)=f_{2}(1)\).
Therefore, in the plane, all paths are homotopic, existing a single homotpy class. Considering the fundamental group, that is only closed paths, we have that all paths are homotopic to the constant path - for its simplicity, the constant path is taken as the representative of the homotopy class.
Formally, given a closed path \(f\) from \([0,1]\) to the plane, the deformation of \(f\) in a constant path (the point \(f(0)\)) can be defined by the homotopy \(H\) from \([0,1]\times[0,1]\) to the plane such that \[H(t,x)=f(0)+x(f(t)-f(0))=\\\;\;\;\;\;\;=(1-x)f(0)+xf(t)\]